Частотные характеристики САР

В условиях реальной эксплуатации САР часто возникает необходимость определить реакцию на периодические сигналы, т.е. определить сигнал на выходе САР, если на один из входов подается периодически сигнал гармонической формы. Решение этой задачи возможно получить путем использования частотных характеристик. Частотные характеристики могут быть получены экспериментальным или аналитическим путем. При аналитическом определении исходным моментом является одна из передаточных функций САР (по управлению или по возмущению). Возможно также определение частотных характеристик. Возможно также определение частотных характеристик исходя из передаточных функций разомкнутой системы и передаточной функции по ошибке.

Если задана передаточная Функция W(S), то путём подставки S=jw получаем частотную передаточную функцию W(jw), которая является комплексным выражением т.е. 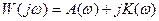, где А(w) вещественная составляющая , а К(w) мнимая составляющая. Частотная передаточная функция может быть представлена в показательной форме:

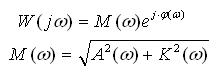
где -модуль;

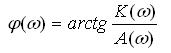
-аргумент частотной передаточной функции

Функция М(w), представленная при изменении частоты от 0 до ¥ получило название амплитудной частотной характеристики (АЧХ).

Функция j(w), представленная при изменении частоты от 0 до ¥ называется фазовой частотной характеристикой (ФЧХ).

Частотная передаточная функция W(jw) может быть представлена на комплексной плоскости. В этом случае для каждой из частот в диапазоне от 0 до ¥ производится определение вектора на комплексной плоскости и строится годограф вектора. Годограф будет представлять собой амплитудно-фазовую частотную характеристику (АФЧХ). Таким образом, для определенной частоты имеем вектор на комплексной плоскости, который характеризуется модулем М и аргументом j. Модуль представляет собой численное отношение амплитуды выходного гармонического сигнала к амплитуде входного. Аргумент представляет собой сдвиг по фазе выходного сигнала по отношению к входному. При этом отрицательный фазовый сдвиг представляется вращением вектора на комплексной плоскости по часовой стрелке относительно вещественной положительной оси, .а положительный фазовый сдвиг представляется вращением против часовой стрелки.

Для упрощения графического представления частотных характеристик, а также для облегчения анализа процессов в частотных областях используются логарифмические частотные характеристики: логарифмическая амплитудная частотная характеристика (л.а.ч.х.) и логарифмическая фазовая частотная характеристика (л.ф.ч.х.). При построении логарифмических характеристик на шкале частот вместо w откладывается lgw и единицей измерения является декада. Декадой называется интервал частот, соответствующий изменению частота в 10 раз. При построений л.а.ч.х. на оси ординат единицей измерения является децибел, который представляет собой соотношение L=20 lg M(w). Для л.ф.ч.х. на оси частот используется логарифмический масштаб, а для углов - натуральный масштаб. На практике логарифмические частотные характеристики строятся на совмещённой системе координат, которые представлены на рис. 3.1.

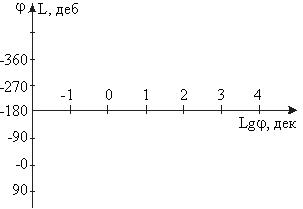
Рис 3.1. Схема координат для логарифмических характеристик