Тригонометрическая и показательная формы комплексного числа

С каждой точкой z = (х, у) комплексной плоскости связан вектор с концом в этой точке и началом в начале координат. Его называют радиус-вектором этой точки, а его длину r называют модулем комплексного числа z и обозначают |z| (см. рисунок 7.5):

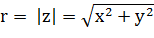
Угол j, образованный радиусом-вектором с осью абсцисс, называют аргументом комплексного числа и и обозначают Arg z
(-p < Arg z ≤ p).

Из рисунка 7.5 видно, что x = r cos j, y = r sin j. Следовательно,

z = r(cos j + i sinj)

Такое представление комплексного числа в виде называют тригонометрической формой комплексного числа.

Свойства арифметических операций над комплексными числами:

1. При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма (рисунок 7.6).

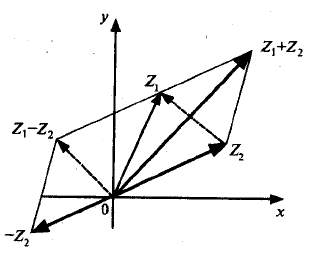
Рисунок 7.6 – Сложение и вычитание комплексных чисел

2. Модуль произведения (частного) двух комплексных чисел равен произведению (частному) модулей этих чисел, а его аргумент - сумме (разности) аргументов этих чисел, т.е.

если z = z₁z₂, то |z| = r₁r₂ = |z₁|*|z₂|; Arg z = Arg z₁ + Arg z₂ = j₁ + j₂;

если z = z₁/z₂, то |z| = r₁/r₂ = |z₁|/|z₂|; Arg z = Arg z₁ - Arg z₂ = j₁ - j₂.

Геометрически умножение числа z₁ на z₂ означает изменение длины радиуса-вектора r₁ (или r₂) в r₂ (или r₁) раз и его поворот вокруг начала координат против часовой стрелки на угол j₂(или j₁).

Так как в соответствии с формулами (16.7) и {16.8) при ум-ножении комплексных чисел их модули перемножаются, а аргу-менты складываются, легко получить формулу возведения комплексного числа в натуральную степень п, из-вестную как формула Муаера:

[r(cos ф + /sin ф)Р = rn (cos щ + fsiii /кр). (16.9)

ОПример 16.3. Найти (-1+020

Ре ше ни е. В примере 16.2 мы получили, что -1 + / =

ц*

Зя я"\

= v2| cos— + /sin — I. Поэтому по формуле Муавра (16.9)

(-и/г-

Ы Зя . Зя) V2 cos— + /sin —

I 4 А)

i г-\20Г Г Зя\ ( * Зя"\

= (V2) cod 20-— +/sin 20 —

Пусть

^z±:p(cos\|/+isinv|/).

Тогда, используя определение корня и формулу Муавра (16.9), получим

z=[p(cosv|/+/sin\|/)| =p*(cosm|/+/sin/?\j/)

или

г(сов'ф + /вшф) = pw(cosn\|/ + /sinwv|/).

Отсюда следует, что

рл = г и ЛХ|/ ==ф + 2я&, где keZ

, т.е.

и/- ф + 2пк

Итак, р = Щг и \|/ = , к е Z,

f Ф+2яА # . ф+2я&

^г =^г(со8ф+/8Шф) =^Н cos +/sin 1, (16.10)

где к— 0, 1, 2,..., я—1.

При £= л, л+1, ... значения корня уже будут повторяться.

Таким образом, корень п-ой степени из комплексного числа (не равного нулю) имеет п различных значений.

^Пример 16.4. Найти ^-1 + 1.

Р е шен и е. В примере 16.2 было получено

r = -l+/ = V2 cos—+/8Щ—I. По формуле (16.10)

^=^(cos^^+/si„^M), ^0,1,2,

откуда получаем три значения корня

z1=(^+/)1=^[coe~+/eiiijJ,

= 1024(со815я + /sin Ш) = 1024 (-1 + 0/) = -1024. ►

Обратимся к извлечению-корня из комплексного числа.

16'

z3 =(^/1+7)з =Щсо&—+пт-^.

if

На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки zb ?2, ?ь расположенные на окружности

радиуса ^2 (рис. 16.3)>>

Связь между тригонометрическими и показательными функциями выражается формулой Эйлера1.

1Г*=5с<Жф + /sintp. (16.11)

Рис. 16.3

Отсюда следует показательная форма комплексного числа:

z = re»y (16.12)

где г-И, Ф = Argz.

В заключение отметим, что в показательной форме, так же как и в тригонометрической, легко проводить операции умножения, деления, возведения в степень, извлечение корня из комплексных чисел.

[1] Рассмотренный способ приведения квадратичной формы к каноническому виду удобно использовать, когда при квадратах переменных встречаются ненулевые коэффициенты. Если их нет, осуществить преобразование все равно возможно, но приходится использовать некоторые другие приемы. Например, пусть f(х₁, х₂) = 2x₁х₂ = x₁² + 2x₁х₂ + х₂² - x₁² - х₂² =

= (x₁ + х₂)² - x₁² - х₂² = (x₁ + х₂)² – (x₁² - 2x₁х₂ + х₂²) - 2x₁х₂ = (x₁ + х₂)² –
- (x₁ - х₂)² - 2x₁х₂; 4x₁х₂ = (x₁ + х₂)² – (x₁ - х₂)²; f(х₁, х₂) = 2x₁х₂ = (1/2)*
*(x₁ + х₂)² – (1/2)*(x₁ - х₂)² = f(y₁, y₂) = (1/2)y₁² – (1/2)y₂², где y₁ = х₁ + х₂, а
y₂ = х₁ – х₂.

[2] Здесь в слове «комплексное» ударение ставится на втором слоге.