Проверка гипотезы о нормальном законе распределения по критерию Пирсона

Для проверки соответствия эмпирического ряда распределения нормальному закону используют критерий 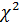, основанный на сравнении эмпирических частот 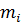с теоретическими 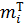, которые можно ожидать при принятии определенной нулевой гипотезы.

Значение 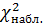- наблюдаемое значение критерия, полученное по результатам наблюдений, равно

,

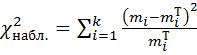Где k – число интервалов (после объединения), 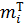- теоретические частоты. Все вспомогательные расчеты, необходимые для вычисления 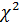, сведём в табл. 6.

Таблица 6

Вычисление критерия 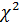при проверке нормальности распределения линейных размеров диаметра втулок

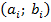
Интервалы	Частота
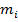
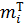
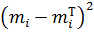
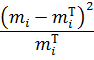
4,97 – 5,08 5,08 – 5,19 5,19 – 5,30	17	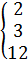15	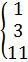	0,267
5,30 – 5,41				0,190
5,41 – 5,52				0,148
5,52 – 5,63				0,727
5,63 – 5,74 5,74 – 5,85	17	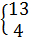15	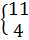	0,267
			-

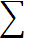
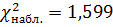
Правило проверки гипотезы заключается в следующем. Определяем по таблице распределения 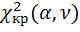хи - квадрат критическое значение для числа степеней свободы 𝛎=k-3 и заданного уровня значимости 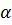. Затем сравниваем 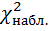и .

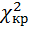Если 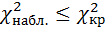, то выдвинутая гипотеза о законе распределения принимается.

Если 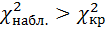, то выдвинутая гипотеза о нормальном законе распределения отвергается с вероятностью ошибки .

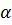Для нашего примера 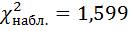, , 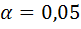𝛎=5-3=2 (число интервалов после объединения стало равным 5) и .

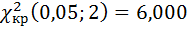Так как 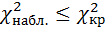, то согласно критерию Пирсона гипотеза о нормальном законе принимается. Можно сделать вывод, что распределение линейных размеров диаметра 100 втулок является нормальным.