Задание 1. Дифракция на одной щели на двух щелях
1. Установите одиночную щель в положение перпендикулярное направлению лазерного пучка (угол  ). При этом стрелка, закрепленная на оси вращения пластинки со щелью, должна указывать на
). При этом стрелка, закрепленная на оси вращения пластинки со щелью, должна указывать на  .
.
2. Получите дифракционную картину от одиночной щели и зарисуйте.
3. Определите координаты положения минимума 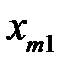 и максимума
и максимума  первого порядка, т.е. измерьте расстояние от центра дифракционной картины до центра первого минимума и до центра первого максимума.
первого порядка, т.е. измерьте расстояние от центра дифракционной картины до центра первого минимума и до центра первого максимума.
4. Поверните щель на угол 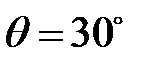 и далее на угол
и далее на угол 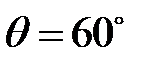 по отношению к первоначальному положению. Пронаблюдайте изменения дифракционной картины и зарисуйте её.
по отношению к первоначальному положению. Пронаблюдайте изменения дифракционной картины и зарисуйте её.
5. Определите координаты положения минимума и максимума первого порядка при углах  и
и  . Все данные занесите в таблицу.
. Все данные занесите в таблицу.
6. Повернув турель 2, установите на место одиночной щели пластинку с двумя щелями. Убедитесь, что плоскость пластинки перпендикулярна световому пучку (угол  ). Зарисуйте дифракционную картину.
). Зарисуйте дифракционную картину.
7. Определите координаты положения первого дифракционного минимума 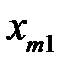 и главного интерференционного максимума первого порядка
и главного интерференционного максимума первого порядка 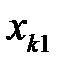 при углах
при углах  ,
,  и
и  для двойной щели. Данные занесите в таблицу.
для двойной щели. Данные занесите в таблицу.
8. Выключите лазерный источник света.
Таблица 1
| одиночная щель | двойная щель | ||||
угол 
| 
| 
| угол 
| 
| 
|
| 
| ||||

| 
| ||||

| 
|
9. По формулам (1) рассчитайте ширину a одиночной щели при угле  и при углах
и при углах 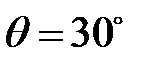 и
и 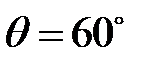 учитывая, что при наклонном падении эффективный (кажущийся) размер ширины щели
учитывая, что при наклонном падении эффективный (кажущийся) размер ширины щели 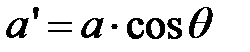 .
.
 ,
, 
 ,
, 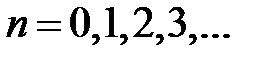 (1)
(1)
где  и
и  – координаты
– координаты 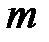 -го минимума и
-го минимума и 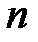 -го максимума,
-го максимума,  – длина волны лазерного излучения,
– длина волны лазерного излучения,  – ширина щели,
– ширина щели, 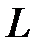 – расстояние от щели до экрана (
– расстояние от щели до экрана (  0,65мкм;
0,65мкм;  370 мм).
370 мм).
10. Запишите результат в формате:
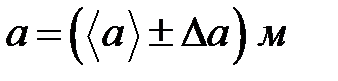
11. По формулам (2) для двойной щели рассчитайте ширину щелей  и расстояние между ними
и расстояние между ними  , приняв во внимание что
, приняв во внимание что 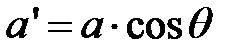 и
и  .
.
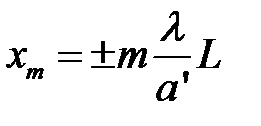 ,
, 
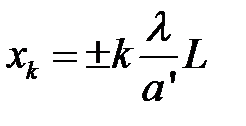 ,
,  (2)
(2)
12. Оцените погрешность измерений по формуле Стьюдента и запишите результат в формате:
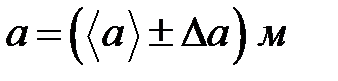
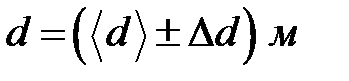
Дата добавления: 2021-05-28; просмотров: 503;











