Работа газа при расширении. Теплота. Удельная и молярная теплоёмкости.

Теплоёмкость при постоянных давлении и объёме. Уравнение Майера.

Внутренняя энергия может изменяться двумя способами: за счёт совершения системой работы и при теплообмене. Рассмотрим газ, находящийся под поршнем в цилиндре (рис.1).

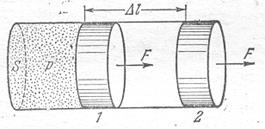
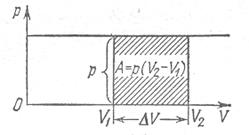
Рис.1 Рис.2

Подвергнем находящийся под поршнем газ изобарному нагреванию.

Согласно закону Гей-Люссака, нагреваясь, газ будет расширяться, передвигая при этом поршень, а, значит, действуя на него с некоторой силой F.

Совершаемую при расширении работу газа можно определить, используя известную формулу для работы: .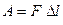

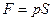Учитывая, что , и 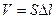, получим выражение для определения работы, совершаемой газом при изобарном расширении

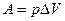. (5)

Графически эта работа может быть представлена площадью фигуры, ограниченной линией давления. При постоянном давлении это прямоугольник, отмеченный штриховкой.

В случае, когда давление непостоянно р ≠ const, работа определяется по формуле

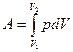. (6)

Внутренняя энергия, отданная или полученная системой в результате теплообмена, называется количеством теплоты или теплотой.

Количество теплоты Q пропорционально изменению температуры 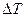системы и определяется из выражений 7 и 8:

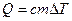, (7)

где m – масса тела, с – удельная теплоёмкость вещества

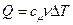, (8)

где 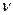- количество вещества, 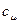- молярная теплоёмкость.

Удельная теплоёмкость – это величина, численно равная количеству теплоты, необходимое для увеличения температуры тела на один градус. Зависит теплоёмкость от рода вещества и от его температуры (что обычно не учитывается).

Для молярной теплоёмкости справедливо аналогичное определение, только вещество берётся в количестве одного моля. Теплоёмкость зависит не только от рода вещества, но и способа теплопередачи.

При изохорном процессе молярная теплоёмкость с_v равна:

,

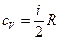где i – число степеней свободы молекул вещества, R – молярная газовая постоянная.

При изобарном процессе молярная теплоёмкость с_p равна:

.

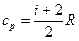Несложно заметить, что 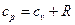- уравнение Майера. (9)