Магнетизм и магнетики.
При движении электрически заряженных частиц между ними возникает особого рода взаимодействие, которое называется магнетизм. Например, при вращении электрона (электрически отрицательно заряженная частица) вокруг атомного ядра, возникает орбитальный магнитный момент. Минимальный орбитальный момент определяется выражением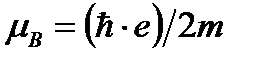 
и называется магнетоном Бора (ħ – постоянная Планка деленная на 2p, е – заряд электрона, m – его масса). Кроме того, электрон вращается вокруг собственной оси, создавая при этом дополнительный спиновый магнитный момент (от английского слова «spin» – «вращаться»). Из этого примера следует два вывода: первый – магнитными свойствами обладают все вещества, второй – электричество и магнетизм являются проявлением одной силы – электромагнетизма (теория Максвелла).
Пространство, в котором, действуют силы магнетизма, называется магнитным полем. Количественной характеристикой магнитного поля является его напряженность и называется магнитной индукцией (B). В вакууме величина магнитной индукции может быть определена по закону Био-Савара-Лапласа. Этот закон ниже приведен в модульной форме.
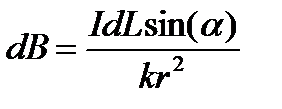
dB – магнитная индукция, которая создается проводником длинной dL, по которому протекает ток силой I. В системе СИ k = 4p. a – угол между dL и направлением на точку, где определяется dB, r – расстояние до точки где определяется B.
Согласно приведенному выше закону электрический ток является единственным источником магнитного поля.
Для объяснения намагничения тел Ампер предложил, что в молекулах вещества циркулируют круговые токи, которые обладают магнитным моментом и создают в окружающем пространстве магнитное поле. В отсутствие внешнего поля (Н = 0) молекулярные токи ориентированы хаотично, вследствие чего обусловленный ими результирующий магнитный момент равен нулю (∑Рmi = 0). Под действием поля (Н ≠ 0) магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего суммарный магнитный момент вещества становится отличным от нуля (∑Рmi ≠ 0) – вещество намагничивается.Намагниченность магнетика принято характеризовать магнитным моментом единицы объема. Эту величину называют вектором намагничения (или намагниченности)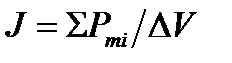
(суммирование производится по объему ΔV). Величина вектора намагничения зависит от намагничивающего поля и может быть выражена следующим соотношением:  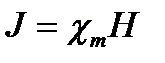| (1) |
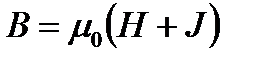 | (2) |
 |
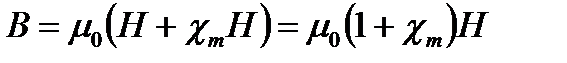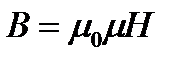 | (3) |
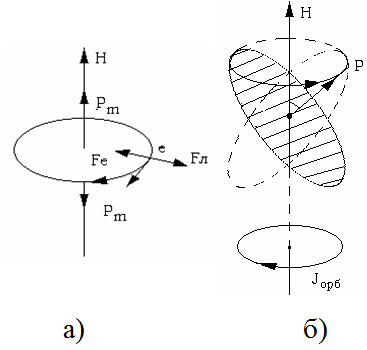Влияние магнитного поля на движение электронов в атомах вещества упрощенно состоит в следующем. В магнитном поле на движущийся электрон помимо силы Fe со стороны ядра действует еще сила Лоренца Fл (рис. 1). Если плоскость орбиты электрона перпендикулярна магнитному полю Н, то это приводит к изменению центростремительной силы, действующей на электрон, и, как следствие этого, к изменению угловой скорости его вращения по орбите. Если же орбита электрона расположена произвольным образом относительно вектора Н, так, что орбитальный магнитный момент электрона составляет с вектором Н угол α, то влияние поля оказывается более сложным. В этом случае вся орбита приходит в такое движение, при котором угол α сохраняется неизменным, а вектор Pm вращается вокруг направления Н с определенной угловой скоростью. Такое движение в механике называется прецессией. Изменение угловой скорости вращения электрона или, в общем случае, появление прецессии эквивалентно дополнительному орбитальному току ΔIорб. (рис. 1, а), б)), которому соответствует индуцированный орбитальный момент электрона ΔPm. Этот вектор противоположен по направлению вектору напряженности магнитного поля Н. Если в атоме имеется несколько электронов, то общий индуцированный орбитальный момент атома равен векторной сумме индуцированных орбитальных магнитных моментов всех электронов: ΔPm=∑ΔPmi. С помощью этого результата, применимого к атому любого вещества, помещенного в магнитное поле, может быть объяснено явление диа- и парамагнетизма. У диамагнетиков магнитные моменты атомов при отсутствии магнитного поля (Н = 0) равны нулю. При внесении диамагнитного вещества в магнитное поле в каждом его атоме индуцируется магнитный момент, направленный противоположно вектору Н напряженности магнитного поля, и, следовательно, вектор намагничения J также направлен противоположно вектору Н. Рисунок 1. Возникновение индуцированного магнитного момента в случаях: а) плоскость орбиты перпендикулярна вектору Н; б) нормаль к плоскости орбиты составляет угол α с направлением вектора Н.
У парамагнетиков магнитные моменты атомов Pm при отсутствии магнитного поля не равны нулю. В результате прецессии также индуцируется магнитный момент ΔPm, направленный против поля. Однако решающую роль в намагничивании парамагнетика играют столкновения атомов, происходящие в результате теплового движения. Причем толчки в направлении прецессионного вращения увеличивают угол между Pm и Н, а в направлении против прецессионного вращения уменьшают его. Толчки первого типа размагничивают, а второго – намагничивают парамагнетик. Эффект намагничивания будет преобладать над эффектом размагничивания, так как толчки против прецессионного вращения в среднем сильнее толчков противоположного направления (подобно тому, как сила сопротивления, испытываемая человеком, будет больше, когда он бежит против ветра, а не по ветру). Возникающий при этом суммарный магнитный момент парамагнетика ΣPmi (направленный по полю) бывает значительно больше, чем суммарный индуцированный (в результате прецессии) момент ΣΔPmi (направленный против поля). Поэтому результирующий магнитный момент оказывается положительным, и вектор намагничения J направлен вдоль магнитного поля Н. Особый класс магнетиков образуют вещества, у которых магнитная проницаемость в сотни и тысячи раз превышает магнитную проницаемость обычных материалов. Эти вещества получили название ферромагнетиков. К ним относятся железо, никель, кобальт и их соединения и сплавы. Другой отличительной особенностью ферромагнетиков является то, что их намагниченность J зависит от Н нелинейно, причем при больших полях наступает состояние магнитного насыщения. Поскольку зависимость J от Н нелинейна, то и магнитная восприимчивость χm зависит от напряженности. Кроме нелинейной зависимости между J и Н (или между В и Н) для ферромагнетиков характерно также наличие явления гистерезиса (рис. 2). Это явление заключается в том, что процесс намагничения ферромагнетика необратим в большей своей части, поэтому кривая намагничения не совпадает с кривой размагничения.
На рисунке 2 изображена зависимость магнитного момента М ферромагнитного образца от напряжённости Н внешнего магнитного поля (кривая намагничивания). В достаточно сильном магнитном поле образец намагничивается до насыщения (при дальнейшем увеличении поля значение М практически не изменяется, точка А). При этом образец состоит из одного домена с магнитным моментом насыщения Ms, направленным по полю. При уменьшении напряжённости внешнего магнитного поля Н магнитный момент образца М будет уменьшаться по кривой I преимущественно за счёт возникновения и роста доменов с магнитным моментом, направленным против поля. Рост доменов обусловлен движением доменных стенок. Это движение затруднено из-за наличия в образце различных дефектов (примесей, неоднородностей и т.п.), которые закрепляют доменные стенки в некоторых положениях; требуются достаточно сильные магнитные поля для того, чтобы их сдвинуть. Поэтому при уменьшении поля Н до нуля у образца сохраняется так называемый остаточный магнитный момент Mr (точка В).
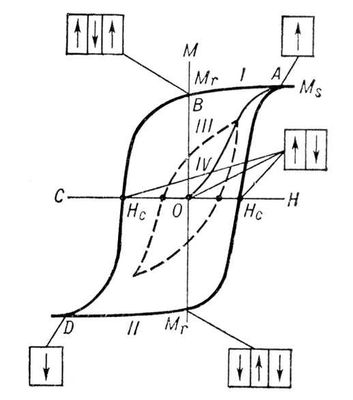Образец полностью размагничивается лишь в достаточно сильном поле противоположного направления, называемом коэрцитивным полем (коэрцитивной силой) Нс (точка С). При дальнейшем увеличении магнитного поля обратного направления образец вновь намагничивается вдоль поля до насыщения (точка D). Перемагничивание образца (из точки D в точку А) происходит по кривой II. Таким образом, при циклическом изменении поля кривая, характеризующая изменение магнитного момента образца, образует петлю магнитного гистерезиса. Если поле Н циклически изменять в таких пределах, что намагниченность насыщения не достигается, то получается непредельная петля магнитного гистерезиса. (кривая III). Уменьшая амплитуду изменения поля Н до нуля, можно образец полностью размагнитить (прийти в точку О). Намагничивание образца из точки О происходит по кривой IV.
Рисунок 2. Петля гистерезиса ферромагнетика
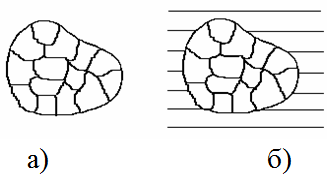Опытами Эйнштейна и де Газа было доказано, что ответственным за магнитные свойства ферромагнетиков являются собственные (спиновые) магнитные моменты электронов (а не орбитальные, как у диа- и парамагнетиков). Атомы элементов, обладающих ферромагнитными свойствами (Fe, Co, Ni), имеют некоторую особенность. В них нарушается последовательность заполнения мест в оболочках и слоях: прежде чем полностью “застроится” нижняя оболочка, начинается заполнение выше расположенной оболочки. В результате электронные спины некоторых внутренних оболочек оказываются нескомпенсированными. Таким образом, ферромагнитными свойствами могут обладать только такие вещества, в атомах которых имеются недостроенные внутренние электронные оболочки. Кроме того, исследования ферромагнитных кристаллов позволили выявить в них области с самопроизвольной (спонтанной) намагниченностью – так называемые домены, линейные размеры которых 1–10 мкм (рис. 3). Рисунок 3. Доменная структура ферромагнетика: а) в отсутствие внешнего поля, б) при наличии внешнего поля.В пределах каждого домена нескомпенсированные спины ориентированы в одном направлении, то есть вещество в домене находится в состоянии магнитного насыщения и обладает определенным магнитным моментом. Направления этих моментов для разных доменов различны, так что в отсутствие внешнего поля суммарный момент всегда равен нулю. Силы, которые заставляют магнитные моменты электронов выстраиваться параллельно друг другу, называются обменными. Их объяснение в рамках классической физики невозможно (дается только квантовой механикой). Если поместить ферромагнетики во внешнее магнитное поле, то вначале, при слабых полях, наблюдается смещение границ доменов. В результате этого происходит увеличение размеров тех доменов, магнитные моменты которых составляют с направление поля Н меньший угол за счет доменов, у которых угол между Pm и H больше. При увеличении Н имеет место поворот магнитных моментов доменов в направлении поля. При этом моменты электронов в пределах домена поворачиваются одновременно, без нарушения параллельности друг другу. Эти процессы являются необратимыми, что и служит причиной гистерезиса. Для каждого ферромагнетика имеется определенная температура Тс, при которой области спонтанного намагничения распадаются и вещество утрачивает ферромагнитные свойства (становится обычным парамагнетиком). Эта температура называется точкой Кюри.
Дата добавления: 2021-05-28; просмотров: 329;
Поиск по сайту
Узнать еще
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
