ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ ТВЕРДЫХ ТЕЛ

Разделим условно все твердые тела на неметаллы и метал­лы. Предположим, что кристаллическая решетка построена из атомов, не имеющих недостроенных внутренних оболочек. Как и в случае неметаллов, решетка проявляет диамагнетизм. На диамагнитный момент внутренних, заполненных оболочек ато­мов близость других атомов влияния не оказывает. Поэтому вклад этих оболочек в результирующий магнитный момент та­кой же, как и у изолированных атомов.

Если в неметаллическом кристалле имеются атомы с час­тично заполненными внутренними оболочками, то вещество представляет собой парамагнетик. Однако магнитный момент незаполненных оболочек в кристалле может отличаться от момента изолированного атома. Поэтому найти парамагнитный момент кристалла путем суммирования моментов всех входя­щих в него свободных атомов в большинстве случаев нельзя.

В металлах вклад в магнитную восприимчивость кроме атомных остовов, расположенных в узлах решетки, вносят кол­лективизированные электроны проводимости. Эксперименталь­ные данные свидетельствуют, например, о том, что все щелоч­ные металлы парамагнитны. При этом их парамагнитная вос­приимчивость не зависит от температуры. Поскольку решетка щелочных металлов диамагнитна, парамагнетизм может быть обусловлен только парамагнетизмом электронного газа. Из независимости парамагнетизма щелочных металлов от темпе­ратуры следует сделать вывод о независимости от температу­ры парамагнитной восприимчивости электронного газа.

Парамагнетизм электронного газа связан с наличием у электронов спинового магнитного момента, равного магнетону Бора. В магнитном поле спиновые магнитные моменты ориен­тируются преимущественно по полю, создавая результирующий магнитный момент. Если для вычисления этого магнитного мо­мента воспользоваться классическими представлениями, то по­лучим, что парамагнитная восприимчивость зависит от темпе­ратуры по закону Кюри. Правильный результат дает теория, разработанная Паули, учитывающая, что электроны в металле подчиняются статистике Ферми—Дирака.

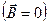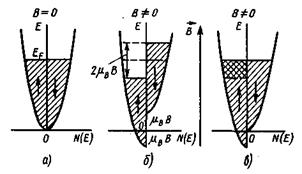
В отсутствие внешнего магнитного поля результи­рующий магнитный момент электронного газа при 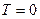К ра­вен нулю. Электроны занимают в зоне проводимости все уровни до уровня Ферми так, что на каждом уровне находится по два электрона с противоположно направленными спинами. Это ил­люстрирует рис. 1.3 а, где зона проводимости разделена на две полузоны, различающиеся направлением спинов.

Рис. 1.3. К расчету парамагнитной восприимчиво­сти электронов проводимости. По оси ординат от­ложена энергия электронов, по оси абсцисс — плотность состояний. Занятые состояния заштри­хованы. Стрелками указаны направления спиновых магнитных моментов

До включения магнитного поля функция плотности состоя­ний 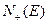электронов со спинами вверх и функции 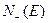для электронов со спинами вниз имеют вид одинаковых парабол. При этом

.

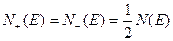В магнитном поле 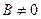полузона, в которой спиновые магнит­ные моменты направлены по полю, сместится вдоль оси 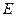вниз на 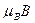, а полузона с противоположным направлением спино­вых магнитных моментов — вверх на 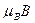. Таким образом, обе полузоны сместятся друг относительно друга на 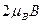(рис. 1.3, б). Так как система стремится к минимуму энергии, то часть электронов из правой полузоны перетечет в левую, изменив при этом направление спина (рис. 1.3, в). В резуль­тате появится магнитный момент, направленный по полю:

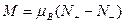, (1.10)

где 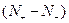— число мигрировавших электронов;

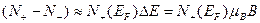. (1.11)

Зная выражение для плотности состояний, легко получить па­рамагнитную восприимчивость электронного газа:

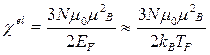. (1.12)

Здесь 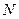— число электронов проводимости в единичном объ­еме металла; 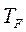— температура вырождения электронного га­за. По определению,

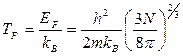. (1.13)

Так как 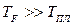(где 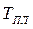— температура плавления металла), 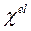не зависит от температуры, поскольку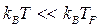

Значение парамагнитной восприимчивости, вычисленное по (1.12), лишь немного больше, чем диамагнитная восприимчи­вость внутренних заполненных оболочек атомов. Поэтому пол­ная магнитная восприимчивость нормальных (т. е. непереход­ных) металлов лишь немного больше нуля. Более того, имеется ряд металлов, которые, несмотря на парамагнитный вклад электронного газа, в целом диамагнитны. Это иллюстрируются табл. 1.2.

Одной из причин результирующего диамагнетизма некото­рых металлов является то, что в них из-за малой плотности со­стояний невелик парамагнетизм электронного газа. Такая ситуация имеет место, например, в бериллии. Атомы бе­риллия имеют по два валентных электрона. Таким образом, валентная зона в бериллии заполнена полностью. Если бы она не перекрывалась со следующей разрешенной зоной, то берил­лий был бы диэлектриком. Металлические свойства бериллия связаны с перекрытием зон. Такое перекрытие есть, но оно не­велико и плотность состояний на уровне Ферми также невели­ка. Поэтому парамагнитная восприимчивость электронного газа мала и бериллий обнаруживает диамагнетизм.

Другой причиной результирующего диамагнетизма метал­лов является большое число электронных орбит в атомах и большие радиусы этих орбит (Сu, Ag, Au, Zn, Ga и т. д.).

Таблица 1.2. Магнитная восприимчивость нормальных металлов

Металл	Атомный номер элемента		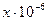Металл	Атомный номер элемента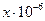
Li Na К Rb Cs Cu Ag Au Be Mg Ca Sr Ba Zn		+1,89 +0,68 +0,47 +0,33 +0,42 -0,76 -2,1 -29 -1,83 +0,95 +1,7 +2,65 +0,56 -1,24	Cd Hg Al Ga In -Tl Sn(белое) Sn(серое) Pb As Sb Te Bi		-1,52 -2,25 +1,67 -1,84 -0,8 -3,37 +0,276 -0,184 -1,36 -0,42 -5,9 -2,0 -13,0

Отметим, наконец, что электроны проводимости обладают не только парамагнетизмом, но и диамагнетизмом. Согласно классической теории, диамагнетизм электронного газа должен быть равен нулю. Это вытекает, например, из энергетических соображений. Магнитное поле искривляет траектории движе­ния электронов проводимости, не изменяя, однако, модуля их скорости. Поэтому при включении магнитного поля кинетиче­ская энергия электронов не изменяется.

Учет квантовых свойств электрона позволил Л. Д. Ландау открыть диамагнетизм электронного газа. Он показал, что диа­магнитная восприимчивость электронного газа

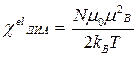, (1.14)

т. е. составляет одну треть от его парамагнитной восприимчи­вости.

Следовательно, полная магнитная восприимчивость электрон­ного газа

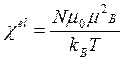. (1.15)

В заключение отметим, что у многих твердых парамагнети­ков температурная зависимость магнитной восприимчивости описывается не законом Кюри, а законом Кюри—Вейсса:

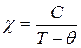. (1.16)

Здесь 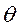— некоторая температура, положительная или отрица­тельная. Зависимость вида (1.16) связана с появлением в этих веществах при 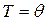ферромагнетизма или антиферромагне­тизма.