Распространение света в двухосных кристаллах.
Теперь исследуем главные следствия основного уравнения (1) для общего случая двухосного кристалла. Оно поможет нам наглядно представить поверхность нормалей, если вначале мы рассмотрим сечения этой поверхности тремя координатными плоскостями 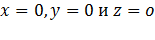 нашей исходной системы (главные диэлектрические оси). Для определенности будем считать, что
нашей исходной системы (главные диэлектрические оси). Для определенности будем считать, что
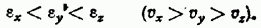 (5)
(5)
Если в уравнении (1) положить 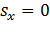 , то оно распадется на два, а именно
, то оно распадется на два, а именно
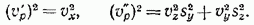 (6)
(6)
Положим 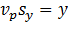 ,
, 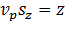 , тогда
, тогда 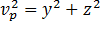 , и уравнения (6) примут вид
, и уравнения (6) примут вид
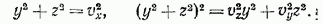 (6а)
(6а)
Таким образом, в сечении поверхности нормалей координатной плоскостью 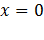 , получаются окружность и овал. В сечении каждой из оставшихся двух координатных плоскостей также получаются окружность и овал, причем единственное различие заключается в относительном расположении этих двух кривых.
, получаются окружность и овал. В сечении каждой из оставшихся двух координатных плоскостей также получаются окружность и овал, причем единственное различие заключается в относительном расположении этих двух кривых.
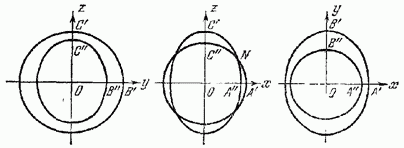
Рис. 3 Сечения поверхности нормалей двухосного кристалла.
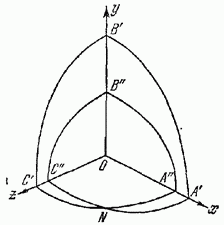
Рис. 4 Поверхность нормалей двухосного кристалла.
При выборе осей, заданном (5), вся окружность расположена вне овала в плоскости 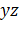 и внутри него в плоскости
и внутри него в плоскости 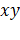 . В плоскости
. В плоскости 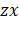 окружность и овал пересекаются в четырех точках (рис. 3). На рис. 4 в перспективе показана часть поверхности нормалей, стягиваемая кривыми
окружность и овал пересекаются в четырех точках (рис. 3). На рис. 4 в перспективе показана часть поверхности нормалей, стягиваемая кривыми 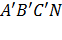 и
и 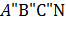 . В общем случае две поверхности пересекаются по кривой, но в нашем случае они имеют лишь четыре общие точки: точку
. В общем случае две поверхности пересекаются по кривой, но в нашем случае они имеют лишь четыре общие точки: точку 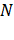 и соответствующие точки в других квадрантах. Две линии, соединяющие начало координат с каждой из этих точек, являются двумя оптическими осями волновых нормалей. Из геометрической теоремы о числе центральных круговых сечений эллипсоида, следует, что не существует других таких точек и, значит, других оптических осей волновых нормалей. Мы подтвердим это прямым расчетом и одновременно выведем неравенство, которое понадобится нам в дальнейшем.
и соответствующие точки в других квадрантах. Две линии, соединяющие начало координат с каждой из этих точек, являются двумя оптическими осями волновых нормалей. Из геометрической теоремы о числе центральных круговых сечений эллипсоида, следует, что не существует других таких точек и, значит, других оптических осей волновых нормалей. Мы подтвердим это прямым расчетом и одновременно выведем неравенство, которое понадобится нам в дальнейшем.
Пусть
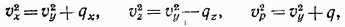 (7)
(7)
где 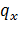 и
и 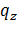 положительны (см.(5)). При такой замене уравнение (1) примет вид
положительны (см.(5)). При такой замене уравнение (1) примет вид
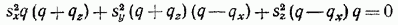 (8а)
(8а)
или
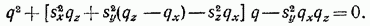 (8б)
(8б)
Так как постоянный член 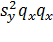 не может быть положительным, корни этого уравнения должны быть вещественными. Если мы обозначим их через
не может быть положительным, корни этого уравнения должны быть вещественными. Если мы обозначим их через 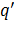 и
и 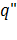 то найдем
то найдем
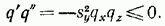
Следовательно, 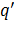 и
и 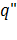 должны иметь разные знаки. Пусть
должны иметь разные знаки. Пусть 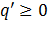 , а
, а 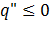 .
.
Если 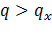 или
или 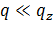 то все члены слева в уравнении (8а) положительны. Следовательно, значения
то все члены слева в уравнении (8а) положительны. Следовательно, значения 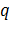 должны лежать в интервале
должны лежать в интервале 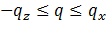 , таким образом,
, таким образом,
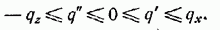 (9)
(9)
Два корня 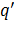 и
и 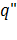 могут быть равными, только если оба они равны нулю. Тогда,
могут быть равными, только если оба они равны нулю. Тогда,
согласно (86), мы должны иметь одновременно
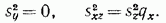 (10)
(10)
Таким образом, мы получили два направления  для каждого из которых соответствующие две скорости равны, что подтверждает существование двух оптических осей волновых нормалей. Как уже было отмечено ранее, эти оси лежат в плоскости
для каждого из которых соответствующие две скорости равны, что подтверждает существование двух оптических осей волновых нормалей. Как уже было отмечено ранее, эти оси лежат в плоскости 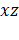 . Если
. Если 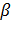 — угол, который образует одна из осей с направлением
— угол, который образует одна из осей с направлением  то
то 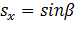 и
и 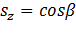 ,где, согласно (10),
,где, согласно (10),
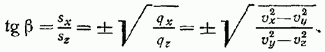 (11)
(11)
Таким образом, оптические оси расположены симметрично относительно оси  Неравенства (9) можно записать через скорости, т. е.
Неравенства (9) можно записать через скорости, т. е.
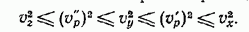 (12)
(12)
Это соотношение понадобится нам в дальнейшем. Мы видим, что обе фазовые скорости вещественны для любого направления волновой нормали. Такое же заключение вытекает, разумеется, из геометрического построения для фазовых скоростей с привлечением эллипсоида волновых нормалей.
Выражение для двух фазовых скоростей, соответствующих заданному направлению волновой нормали  , принимает очень простую форму, если
, принимает очень простую форму, если  , определить через углы
, определить через углы 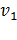 и
и 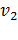 которые эта нормаль образует с двумя оптическими осями волновых нормалей. Поскольку направляющие косинусы оптических осей равны
которые эта нормаль образует с двумя оптическими осями волновых нормалей. Поскольку направляющие косинусы оптических осей равны 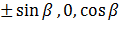 , углы
, углы 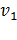 и
и 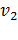 определяются соотношениями
определяются соотношениями
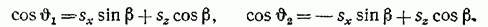 (13)
(13)
Корни уравнения (86), выраженные через 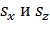 имеют вид
имеют вид
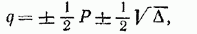 (14)
(14)
где, если воспользоваться тождеством 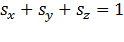
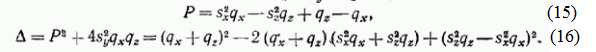
Но из (13) и (11) имеем
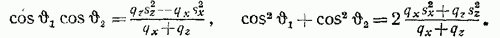 (17)
(17)
Следовательно, выразив (15) и (16) через 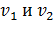 получим
получим
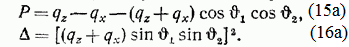
Подставляя (15а), (16а) в (14) и заменяя 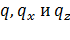 их значениями из выражений (7), окончательно находим
их значениями из выражений (7), окончательно находим
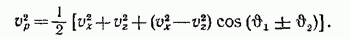 (18)
(18)
Хотя в последнее уравнение и не входит 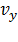 , оно неявно содержится в
, оно неявно содержится в 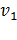 и
и 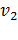 , так как эти углы зависят от угла
, так как эти углы зависят от угла 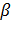 , являющегося функцией всех трех главных скоростей.
, являющегося функцией всех трех главных скоростей.
В частном случае одноосного кристалла 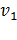 и
и 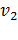 равны. Легко показать, что тогда уравнение (18) точно переходит в (4).
равны. Легко показать, что тогда уравнение (18) точно переходит в (4).
Подобный анализ применим и к лучам. Начав с лучевого уравнения 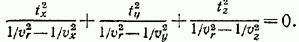 , мы найдем, что в сечении лучевой поверхности координатной плоскостью
, мы найдем, что в сечении лучевой поверхности координатной плоскостью 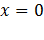 получаются две кривые
получаются две кривые
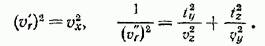 (19)
(19)
Если положить 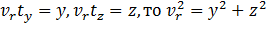 , и (19) примет вид
, и (19) примет вид
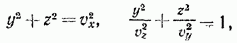
т. е. сечение лучевой поверхности плоскостью 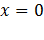 дает окружность и эллипс (а не овал — кривую более общего типаа, как в случае (6а)). Каждое из сечений двумя другими координатными плоскостями также представляет собой окружность и эллипс. В соответствии с неравенством (5) в плоскости
дает окружность и эллипс (а не овал — кривую более общего типаа, как в случае (6а)). Каждое из сечений двумя другими координатными плоскостями также представляет собой окружность и эллипс. В соответствии с неравенством (5) в плоскости 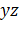 эллипс находится внутри окружности, тогда как в плоскости
эллипс находится внутри окружности, тогда как в плоскости 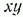 он охватываег окружность. В плоскости
он охватываег окружность. В плоскости 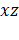 окружность и эллипс пересекаются в четырех точках. Эти точки указывают положение лучевых оптических осей
окружность и эллипс пересекаются в четырех точках. Эти точки указывают положение лучевых оптических осей 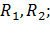 их направления определяются соотношениями, соответствующими соотношениям (10), а именно
их направления определяются соотношениями, соответствующими соотношениям (10), а именно
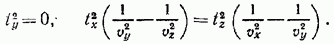
Угол 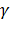 между каждой из этих осей и осью
между каждой из этих осей и осью  поэтому определяется выражением
поэтому определяется выражением
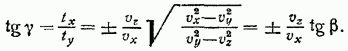
Если 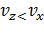 лучевая оптическая ось образует меньший угол с осью
лучевая оптическая ось образует меньший угол с осью  чем ось нормалей.
чем ось нормалей.
Дата добавления: 2017-01-08; просмотров: 1377;










