Задания для практических занятий
Задание 1. Определите на основе нижеприведённых данных степень неравномерности поставок продукции, используя метод среднего квадратичного отклонения:
| Квартал | План поставки, тыс.руб. | Фактически поставлено, тыс.руб. | Выполнение плана поставки, % (х) | Отклонение фактического уровня от планового, % (х – 100) | (х – 100) 2 | Веса (f) гр.2,сокращен- ные в 100 раз) | ∑ (х – 100)2 х х(f) (гр.6х7) |
| 1 050 | |||||||
| ИТОГО | ? | ? |
Среднее квадратичное отклонение σ исчисляют по формуле
σ = 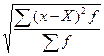 ,
,
где х– конкретное значение признака;
Х – среднее значение признака;
f – вес каждого значения признака.
Под равномерностью поставок понимают выполнение плана поставок продукции в сроки и в объёмах, предусмотренных договором о поставке. Показатель среднего квадратичного отклонения при этом будет характеризовать средний размер отклонений фактических процентов выполнения плана поставок за отрезки отчётного периода (х) от планового уровня (100 %).
С учётом указанных условий формула для исчисления показателя неравномерности поставок (Кнеравн.пост. ) будет иметь следующий вид:
Кнеравн. Пост. = 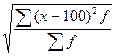 ,
,
где х– фактическое выполнение плана поставок (%) за отрезки отчётного периода;
100 – плановый уровень поставки за каждый отрезок отчётного периода, %;
(х – 100) – отклонение фактического уровня поставки от планового за отдельные отрезки отчётного периода, %;
f – веса отклонений за отдельные отрезки отчётного периода, в качестве которых должны быть взяты плановые размеры поставок.
Задание 2. Определите оптимальный объём партии заготовок станкосборочного цеха (Р), оптимальный интервал между поставками (Т), суммарные годовые затраты (З), если дано:
1. Спрос (потребность) цеха в заготовках: р = 35 000 шт. в год;
2. Издержки размещения заказа: И = 50 ден.ед;
3. Удельные издержки хранения: д = 5 ден.ед.;
Для решения используйте следующие модели:
а) оптимальный объём партии заготовок (вычисление из корня) Р = 2*И*р / д или Р = 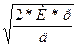 ;
;
б) оптимальный интервал времени между поставками (вычисление из корня)
Т= 2*И / д*р или Т = 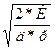 ;
;
в) суммарные годовые затраты З= д*Р.
Задание 3. Используя корреляционно-регрессионный способ анализа, определите зависимость уровня издержек на ремонт основных средств от срока их эксплуатации, используя следующие данные:
| Период (год) | Сумма издержек, тыс. руб. |
| 1-й | |
| 2-й | |
| 3-й | |
| 4-й | |
| 5-й |
Для решения используйте следующие модели:
а) используя линейную функции, найдите срок эксплуатации (у):
у=а+-вх,
где у – срок эксплуатации;
х – ежегодные затраты;
б) для этой функции даётся общая целевая функция:
Z = ∑ (S – aвx ) – min,
где S – общая сумма издержек на ремонт за пять лет, а для определения от а до в два равенства:
∑ S = х∙а + в∑х;
∑ Sх = ах + в∑х2 ;
в) найдите величины ∑ S, ∑х, Sx, ∑ Sх, x2 и ∑х2 в таблице:
| n (годы) | S | x | Sx | x2 |
| 2 100 | ||||
| 3 000 | ||||
| 3 600 | ||||
| 5 400 | ||||
| 5 900 | ||||
| ∑ |
Дата добавления: 2021-05-28; просмотров: 434;











