Использование ДКП в стандарте кодирования MPEG-2

Цель внутрикадрового кодирования - сокращение пространственной избыточности в пределах кадра (или поля) телевизионного изображения. Эта избыточность вызвана сильными корреляционными связями между элементами изображения. Если найти соответствующее ортогональное преобразование, то можно преобразовать массив отсчетов изображения в матрицу коэффициентов, которые уже не будут коррелированны друг с другом. К этим некоррелированным коэффициентам можно применить энтропийное кодирование и добиться сокращения цифрового потока. Наиболее часто используются методы линейных ортогональных преобразований. Линейность ортогонального преобразования означает, что операции сложения, вычитания и умножения на скаляр действительны и после преобразования, а ортогональность - что преобразуемый фрагмент представляется ограниченным набором ортогональных функций.

Линейные ортогональные преобразования характеризуются тем, что между элементами изображения устраняются статистические зависимости и распределение энергии в преобразованном спектральном фрагменте является неравномерным. Эти особенности используются непосредственно в процессах кодирования. На практике можно подобрать такое ортогональное преобразование, что для типичных изображений большая часть коэффициентов матрицы будет иметь практически нулевые значения. Исключая эти нулевые коэффициенты, можно также сокращать цифровой поток. Среди возможных ортогональных преобразований наиболее широко используется ДКП, основанное на применении ортогональной системы дискретных косинусных функций возрастающей частоты. Преобразования данного типа хорошо согласуются с параметрами телевизионного сигнала, что является необходимым условием эффективного кодирования видеоинформации.

Стандарт MPEG-2 подразумевает применение ДКП составляющих видеосигнала. Например, ДКП действительной последовательности отсчетов х(n) при n = 0,1,…, N-1 определяется соотношением

где коэффициенты c(k)=

Обратное ДКП, восстанавливающее исходную последовательность отсчетов по последовательности коэффициентов преобразования Х_с (k), задается выражением

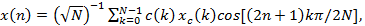
где k=0,1,…, N-1.

ДКП сокращает избыточность и высокочастотную информацию в пределах кадра. Это позволяет получить высокое качество кодированных изображений с сжатием.

ДКП выполняется поблочно, для чего телевизионное изображение разбивается на блоки. При этом в телевизионном кадре создается: 576/8 = 72 зоны по вертикали и 704/8 = 88 зон по горизонтали, что в общей сложности дает 72x88 = 6336 блоков, подлежащих ДКП в реальном масштабе времени. В результате ДКП исходная сигнальная матрица 8 х 8 = 64 телевизионных отсчетов преобразуется в матрицу частотных коэффициентов ДКП такого же размера 8x8 = = 64.

Каждый коэффициент характеризует амплитуду определенной частотной составляющей кадра, причем коэффициенты в матрице располагаются по возрастанию частот в вертикальном и горизонтальном направлениях.

Поскольку положение телевизионных отсчетов сигнальной матрицы определяется двумя координатами, то частотные коэффициенты матрицы ДКП являются функциями этих двух переменных. Следует отметить, что матрица частотных коэффициентов ДКП уже не имеет прямой геометрической связи с положением отсчетов телевизионного сигнала на телевизионном растре, а представляет собой только удобную форму математической записи, при которой частотные коэффициенты ДКП можно трактовать как двумерный спектр телевизионного изображения в горизонтальном и вертикальном направлениях телевизионного кадра.

При этом справедливо и обратное положение - знание матрицы коэффициентов, т.е. значений амплитуд базисных косинусоидальных функций разных частот, позволяет сформировать блок элементов изображения (сигнальную матрицу). Таким образом, ДКП является обратимым.

Спектр ДКП имеет очень важную, если ее оценивать с позиций компрессии видеоданных, особенность: для большинства блоков типичных изображений основная энергия частотных составляющих этого спектра концентрируется в небольшой области около нулевых частот. Например, постоянная составляющая и несколько низкочастотных базисных функций, имеющих значимые величины, отображаются совокупностью коэффициентов ДКП в левом верхнем углу матрицы. Амплитуда высокочастотных составляющих или мала, или просто равна нулю, поэтому их потеря почти не сказывается на качестве изображения. Передаче подлежат только те частотные коэффициенты матрицы ДКП, величины которых превышают принятые пороговые значения, коэффициенты ниже порогового значения считаются нулевыми, что и приводит к желаемой компрессии.

Введение пороговой (нелинейной) обработки, строго говоря, ведет к потерям информации и, соответственно, к снижению качества восстановленного в декодере телевизионного изображения. Однако при разумном выборе величины порог» это ухудшение окажется практически незаметным или же допустимым.

Следует отметить, что при внутрикадровом кодировании динамический интервал коэффициентов ДКП возрастает в 8 раз. Так, при уровневом кодировании видеосигнала восемью битами его динамический интервал равен 0-250 дискретных уровней. При этом динамический интервал коэффициентов спектра ДКП составит от 0 до 2040 и от -1020 до +1020 дискретных уровней для коэффициентов постоянной и переменных составляющих ДКП, соответственно.

Вычисление коэффициентов ДКП с большей точностью, чем имеют значения отсчеты яркости изображения, объясняется необходимостью пренебречь ошибками их определения для исключения возможных неточностей при ДКП.

Кодирование коэффициентов ДКП в таком широком динамическом интервале потребует в последующих узлах кодера перехода от 8-битового к 11-битовому коду. Чтобы избежать этого, после ДКП производится масштабирование (сжатие) динамического интервала сигналов коэффициентов ДКП за счет увеличения шага квантования в 8 раз. Эта операция сводится к делению полученных в матрице значений коэффициентов ДКП на 8. Результат деления затем округляется до ближайших целых значений уровней новой шкалы квантования. Так, например, если исходное значение коэффициента ДКП было 22, то после деления на 8 и округления до ближайшего целого значения (22/8 = 2,75) новое значение будет 3. При этом новый динамический интервал составит от -255 до +255 дискретных уровней.

В обычной ИКМ уменьшение разрядности приводит к возрастанию шумов квантования на всех частотах. Коэффициенты ДКП определяют энергию сигнала на различных частотах, поэтому появляется возможность изменять параметры квантования дифференцировано на разных частотах, учитывая различную чувствительность зрения к разным пространственным частотам.

Коэффициент, соответствующий постоянной составляющей телевизионного сигнала, кодируется с использованием 10 бит, потому что при более грубом квантовании соседние блоки начинают отличаться по яркости. На экране они проявляются в виде шахматной структуры.

На предельно большое число уровней квантуются и амплитуды нескольких самых низкочастотных косинусоидальных волн, располагающихся в левом верхнем углу блока ДКП. По мере увеличения частоты косинусоидальных компонент (при удалении от левого верхнего угла блока ДКП) количество уровней квантования уменьшается, достигая для самых больших частот значений в несколько единиц. Например, самая высокочастотная компонента, располагающаяся в правом нижнем углу, может квантоваться всего на два уровня. Это означает, что для ее передачи можно использовать одноразрядные двоичные числа.

Практически квантование выполняется путем поэлементного деления матрицы коэффициентов ДКП на матрицу квантования (взвешивания), значения элементов которой возрастают по мере удаления от левого верхнего угла и приближения к правому нижнему углу. При этом важно отметить, что для квантования сигнала яркости и цветоразностных сигналов используются разные матрицы. Построчные матрицы квантования могут задаваться кодером, но по умолчанию стандарт MPEG-2 предполагает использование следующей эффективной матрицы (табл. 6.4) [12].

Таблица 6.4. Матрица квантования яркостного сигнала для блоков изображений I-кадров

При декодировании на приемной стороне коэффициенты матрицы ДКП, значения которых были переданы по каналам связи, умножаются на элементы матрицы квантования, что восстанавливает верные значения коэффициентов, но с ошибкой округления, значение которой мало для низкочастотных компонентов блока отсчетов изображения, но велико для высокочастотных.

Массив коэффициентов, извлекаемых из матрицы ДКП, содержит некоторое количество нулевых значений. Для того, чтобы способствовать объединению нулевых элементов в группы и преобразованию в одномерную последовательность, используется зигзагообразное сканирование матрицы, начиная с левого верхнего угла. В этом случае коэффициенты выстраиваются в порядке возрастания частот, причем если пространственные частоты одинаковы, то впереди следуют коэффициенты для меньших вертикальных частот.

Зигзаг-сканирование (z-упорядочивание) позволяет сгруппировать самый большой массив нулевых коэффициентов, обычно располагающийся в правой нижней части блока ДКП.

Примером преобразования стандартной сигнальной матрицы 8x8 пикселей может служить процесс ДКП, квантования и зигзагообразного сканирования, графически представленный на рис. 6.18.

Последний алгоритм сокращения избыточности связан с кодами, образующими комбинации переменной длительности. При этом те коэффициенты ДКП, которые повторяются наиболее часто, кодируются короткими кодовыми комбинациями, а редкие значения коэффициентов - более длинными.

Для экономного представления двоичных сообщений в стандарте MPEG-2 используется код Хаффмана, позволяющий практически в 1,22 раза сократить поток данных по сравнению с равномерным кодированием. При кодировании символов сообщения комбинациями переменной длины обычно возникает проблема отделения одной комбинации от другой. Код Хаффмана обладает свойством префиксности, т.е. ни одна его кодовая комбинация не является началом другой комбинации, что позволяет обойтись в тексте кодированного сообщения без разделителей между комбинациями.

Энтропийный кодер в устройстве кодирования с информационным сжатием MPEG-2 должен иметь многокадровый буферный накопитель, в котором происходит накопление данных для их оптимального использования. Например, в случае, если содержание изображения изменяется с очень большой интенсивностью, возможно изменение скорости передачи данных для сохранения соответствующего качества изображения. Однако на практике при передаче и распределении телевизионных программ колебания скорости передачи данных могут быть недопустимы.

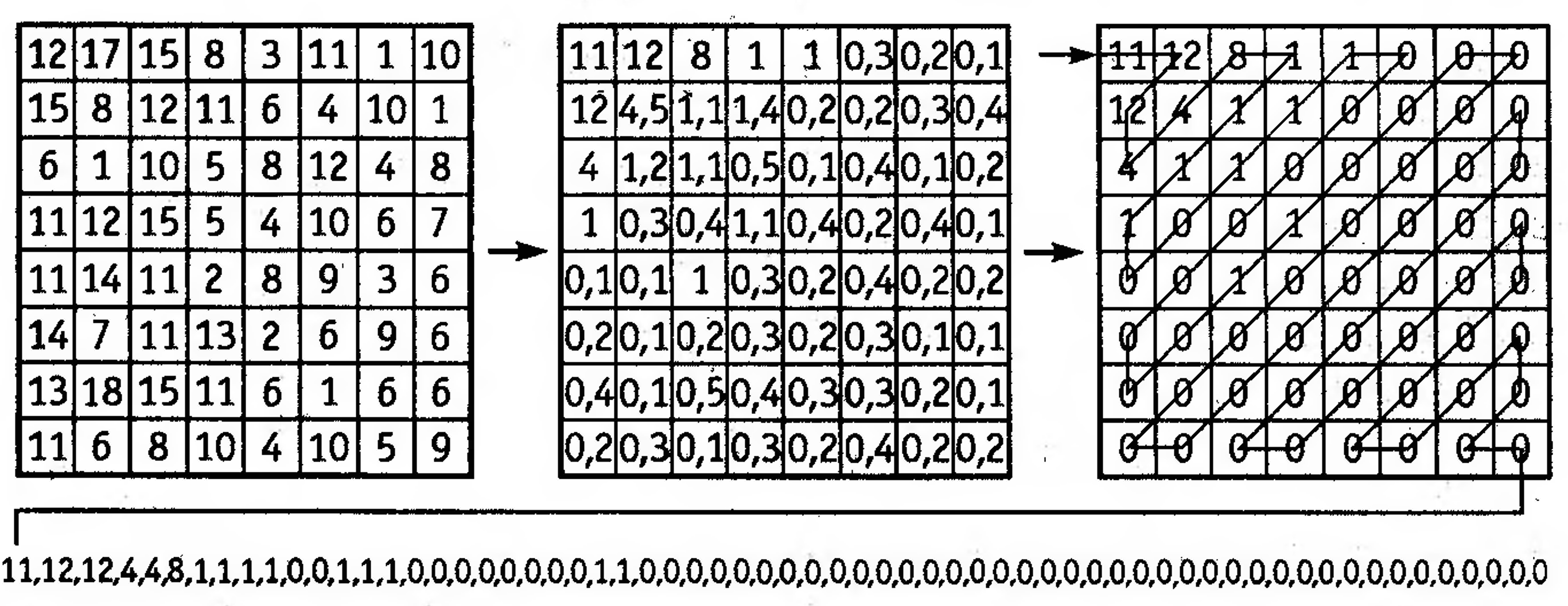
Рис. 6.18. Графическое представление процесса ДКП, квантования и зигзагообразного сканирования в аппаратуре кодирования по стандарту MPEG-2

Рис. 6.19. Графическое представление структуры декодирования в декодерах MPEG-2

В этом случае используется режим работы энтропийного кодера, при котором обеспечивается фиксированная скорость выходного потока данных. Для чего данные заносятся в буферный накопитель с переменной скоростью, а считываются с постоянной. Для предотвращения переполнения буферного накопителя или полного стирания информации в нем, что может привести к сбоям в работе системы видеокомпрессии, используется адаптивное квантование. Сведения о степени заполнения буферной памяти служат сигналом управления, регулирующим шкалу квантования. Если, например, кодируемое изображение характеризуется высокой детальностью, то число ненулевых элементов матриц коэффициентов ДКП увеличивается. Возрастает и объем передаваемых данных, поэтому буферный накопитель заполняется с повышенной скоростью. Благодаря обратной связи (через регулятор скорости потока данных, см. рис. 6.14) квантование становится более грубым и скорость поступления данных в буферную память уменьшается, но за счет увеличения шумов квантования и ухудшения качества изображения. Если кодируется простое по структуре изображение с малой детальностью, то число нулевых элементов сигнальных матриц коэффициентов ДКП увеличивается и скорость поступления данных в буферную память снижается по сравнению со средней величиной. Тогда квантование становится менее грубым (большое число коэффициентов ДКП квантуется на максимальное число уровней). Таким образом, скорость заполнения буферного накопителя в среднем поддерживается на постоянном уровне.

На приемном конце упрощенная структура декодирования графически может быть представлена рис. 6.19.