Характеристики сигналов

1) Длительность первичного сигнала 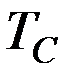– определяющая интервал времени, в пределах которого сигнал существует, т.е. тождественно не равен 0.

2) Постоянная составляющая – среднее значение случайного процесса, определяется как математическое ожидание .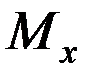

Для эргодического процесса усреднение по времени – усреднения по его реализациям

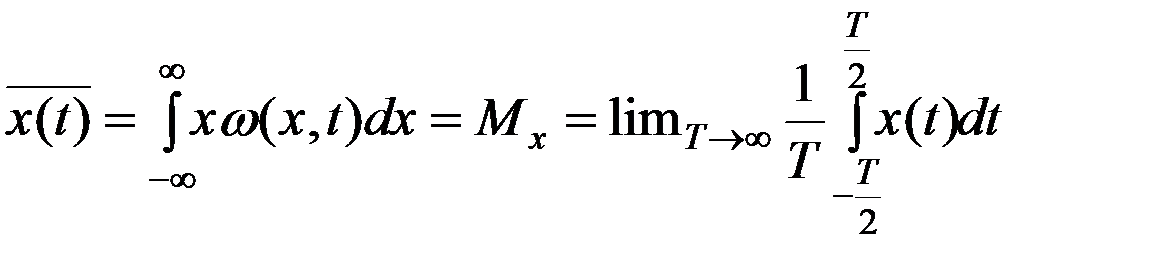
Примечание. Постоянная составляющая не зависит от времени, но является случайной величиной для данной реализаций.

3) Переменная составляющая случайного процесса – центрированный случайный процесс.

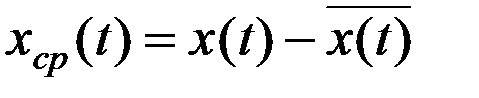
4) Мощность сигнала – среднее значение квадрата мгновенного значения случайного процесса.

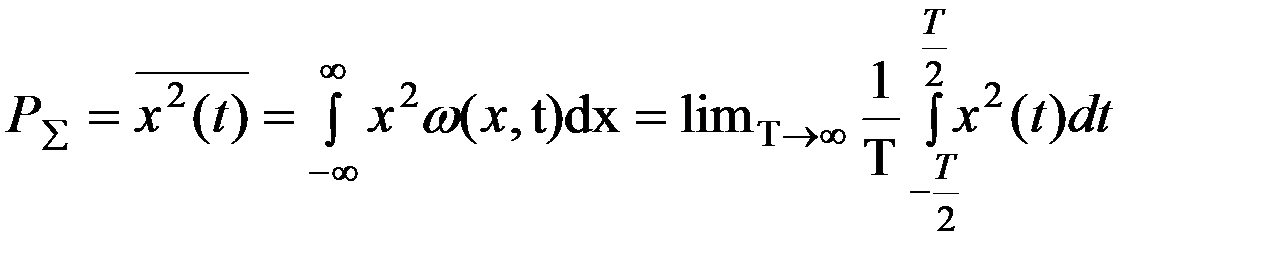
5) Средняя мощность сигнала – мощность переменной составляющей, постоянная составляющая не учитывается, т.к. не несет информации. Совпадает с дисперсией случайного процесса 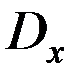, мерой его разброса около среднего значения.

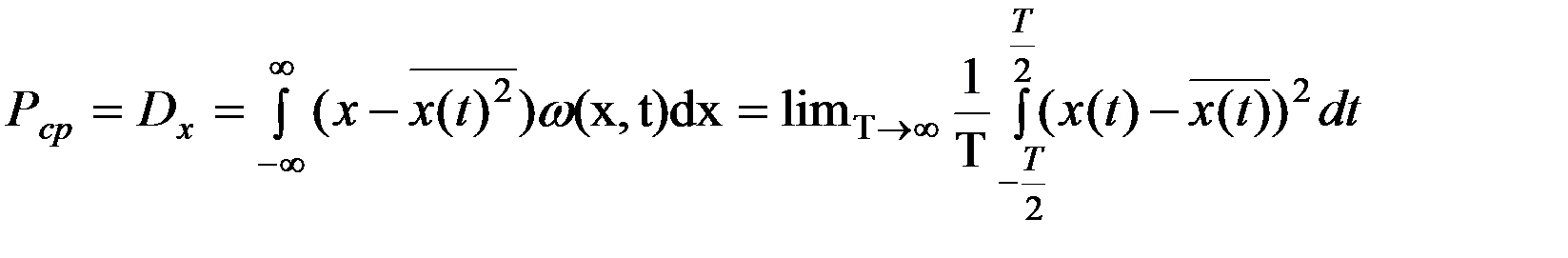
Примечание.Дисперсия численно равна удельной мощности переменной составляющей случайного сигнала на сопротивлении 1 Ом.

6) Максимальная мощность P_max – мощность эквивалентного гармонического сигнала с амплитудой U_m, которая превышается мгновенными значениями переменной составляющей сигнала 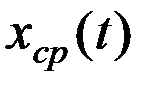с заданной вероятностью ξ= 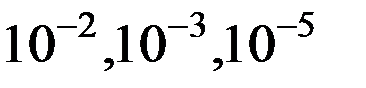в зависимости от сигнала

Примечание.Средняя и максимальная мощности должны быть такими, чтобы при прохождении по каналу передачи не превышались допустимые значения, обеспечивающие неискаженную передачу сигнала.

7) Минимальная мощность P_min – мощность эквивалентного гармонического сигнала с амплитудой U_m, которая превышается мгновенными значениями переменной составляющей случайного сигнала 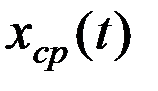с заданной вероятностью (1-ξ)

8) Динамический диапазон 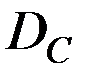характеризует возможный разброс мощностей первичного сигнала в конкретной точке канала:

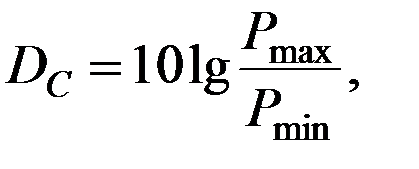дБ

9) Пик-фактор 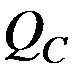характеризует превышение максимальной мощности над средней:

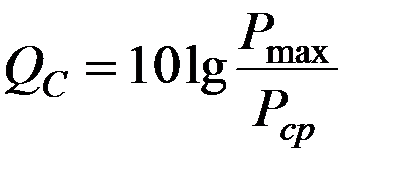, дБ

10) Корреляционная функция случайного процесса характеризует скорость изменения случайного процесса

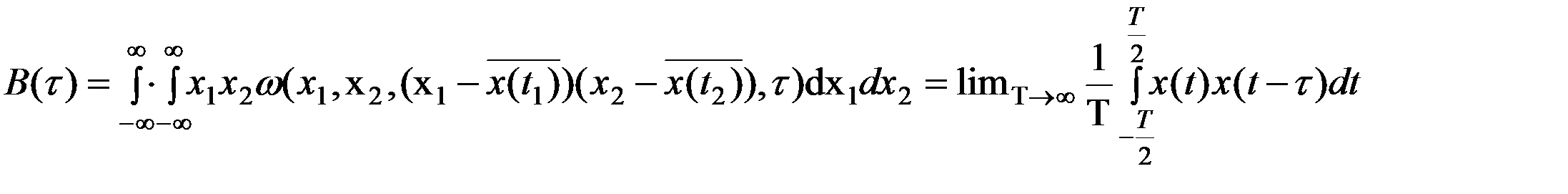При 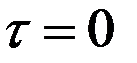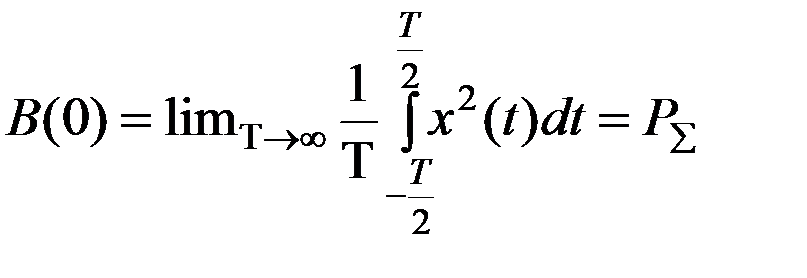и для центрированного случайного процесса = 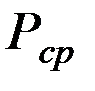полной средней мощности случайного сигнала

Примечание. При 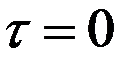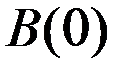-max, т.к. любой сигнал коррелирован сам с собой.

11) Энергетический спектр функции x(t) <=> спектральная плотность средней мощности – это средняя мощность приходящаяся на 1 Гц при заданной частоте.

Согласно теореме Винера-Хинчина энергетический спектр и корреляционная функция связаны преобразованием:

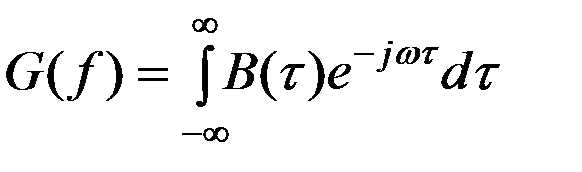- функция четная

Справедливо и обратное преобразование:

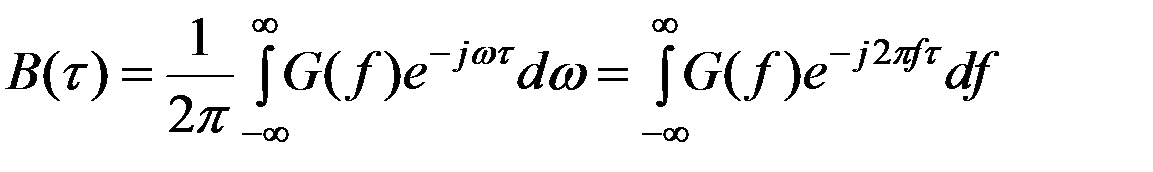
Спектральная плотность характеризует – распределение мощности отдельных спектральных компонент сигнала

При τ(0) 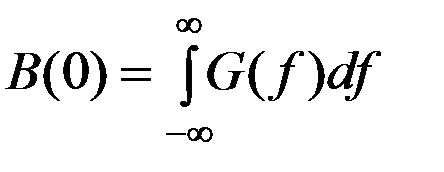- полная мощность сигнала

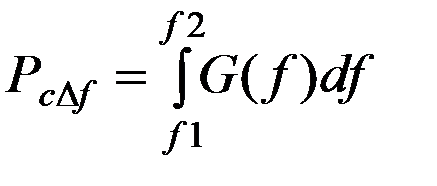- средняя мощность в конечной полосе частот

Примечание. Спектральная плотность – мощность процесса, определена в бесконечно малой полосе частот df вблизи частоты f.

12) Эффективная ширина энергетического спектра сигнала

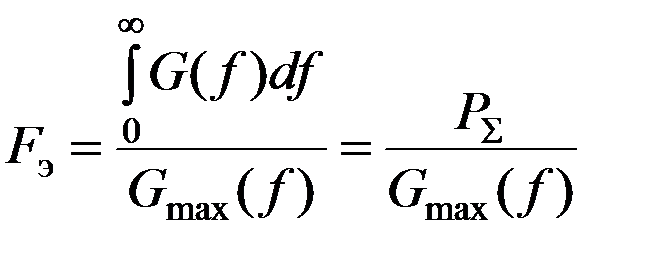
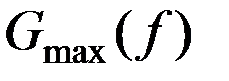-max значение спектральной плотности

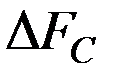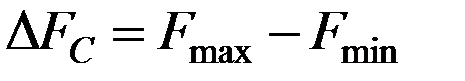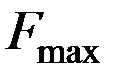Примечание. Вcегда можно указать частотный диапазон , в пределах которого сосредоточена основная энергия сигнала: , где и 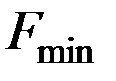-максимальная и минимальная частоты первичного сигнала.

Эффективная ширина энергетического спектра есть эффективно-передаваемая полоса частот (ЭППЧ), которая определяется экспериментально исходя из требований качества передачи для конкретного вида первичного сигнала.

13) Информационная производительность источника – это количество информации, передаваемое в единицу времени

Для цифрового сигнала по формуле Шеннона

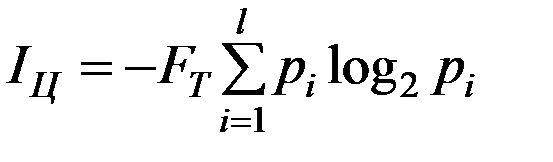, [бит/с]

где -число разрешенных уровней

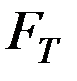-тактовая частота отсчетов

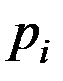- вероятность появления отсчета с i-ым уровнем

Для аналогового сигнала: может быть представлена последовательностью дискретных отсчетов согласна теореме Котельникова ( ):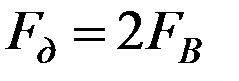

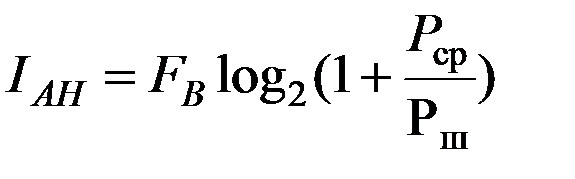, [бит/с]

где 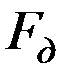- частота дискретизации сигнала

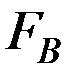-верхняя граничная частота сигнала

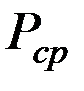-средняя мощность сигнала

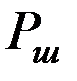- средняя мощность шумовой реализации

14) Объем первичного сигнала :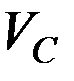

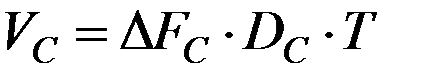
где 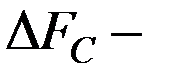эффективно-передаваемая полоса частот

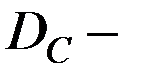динамический диапазон сигнала

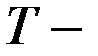время существования сигнала