Помехоустойчивость непрерывной системы связи.
Любое воздействие на сигнал приводит к уменьшению достоверности.
Е2ош = 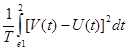 - среднее квадратичное отклонение.
- среднее квадратичное отклонение.
Е2ош 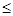 Е2ош доп
Е2ош доп
Факторы, влияющие на помехоустойчивость:
 Помехоустойчивость является функцией отношения сигнала к помехи.
Помехоустойчивость является функцией отношения сигнала к помехи.
2. Зависит от формы сигнала, т.е. от способа модуляции степени различимости сигнала.
3. 0т метода приема и дальнейшего способа обработки сигнала. При известном методе модуляции, способе кодирования и уровне помехи, сообщение можно передавать через систему связи с достоверностью (помехоустойчивостью) не выше некоторого предельного.
Приемник, который обеспечивает предельную помехоустойчивость, называется идеальным (оптимальным, или приемником Котельникова).
Все реальные приемники имеют помехоустойчивость ниже предельной (идеальной). Предельную помехоустойчивость принято называть потенциальной.
Скорость передачи - это количество двоичных символов, передаваемых через канал связи за единицу времени (R).
R =1/τ0 Log2 m , где m - значимость кода
При известном виде модуляции, способе кодирования и уровне помехи через систему связи можно пропускать сообщений не более некоторой величины С.
С — пропускная способность системы связи — предельное количество сообщений, которое можно пропустить через систему связи. R ≤ С
Лекция-8 КЛАССИФИКАЦИЯ РАДИОЭЛЕКТРОННЫХ ЦЕПЕЙ.
Любая система радиосвязи и средства радиоэлектроники состоят из отдельных функциональных узлов, на вход которого подается x(t); на выходе y(t).
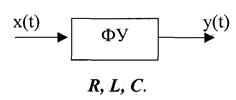
Любой ФУ состоит из резисторов R, конденсаторов С и катушек индуктивности L, соединенных между собой по определенному закону.
Транзисторы, полупроводниковые диоды, лампы заменяются эквивалентными схемами с использованием R, L, С.
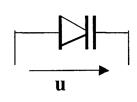
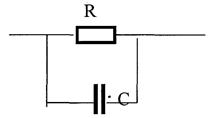
В зависимости от используемых элементов (элементной базы) различают следующие виды радиоэлектронных цепей:
1. Линейные электрические цепи (ЛЭЦ).
а) К ЛЭЦ применим принцип суперпозиции - отклик на суммарное воздействие равно сумме откликов на каждое воздействие в отдельности.
б) В ЛЭЦ не происходит обогащение спектра, т.е. не появляются новые спектральные составляющие.
2. Нелинейные электрические цепи (НЭЦ). Если электрическая цепь содержит хотя бы один нелинейный элемент, параметры которого зависят от величины тока I, проходящего через него, и от напряжения U , то такая цепь называется нелинейной.
а) К НЭЦ не применим принцип суперпозиции, т.е. отклик на суммарное воздействие не равен сумме отдельных воздействий.
б) В НЭЦ происходит обогащение спектра, т.е. появляются новые спектральные составляющие.

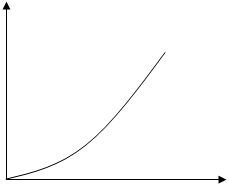
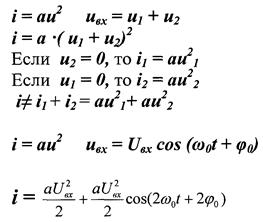 0 u
0 u
Лекция – 9 ПАРАМЕТРИЧЕСКИЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ (ПЭЦ)
Если электрическая цепь содержит хотя бы один элемент R(t), L(t), C(t), параметры которого являются функцией от времени, то такая цепь называется параметрической.
1. К ПЭЦ применим принцип суперпозиции.
exp = u1 + u2
i = exp 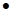 g(t)= u1 g(t) + u2 g(t)
g(t)= u1 g(t) + u2 g(t)
g(t) = g0 (1 + mgcos 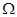 t)
t)
Mg = 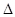 g/go - коэффициент изменения проводимости
g/go - коэффициент изменения проводимости
2. В ПЭЦ происходит обогащение спектра, т.е. появляются новые спектральные составляющие тока. exp (t) = Uex cos (  t+
t+ 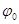 )
)
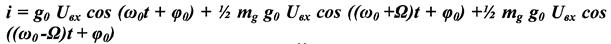
НЕЛИНЕЙНЫЕ ПЭЦ
1. К НПЭЦ неприменим принцип суперпозиции. 2. В НПЭЦ происходит обогащение спектра.
Лекция-10 ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Все элементы R, L, С, при помощи которого определяется эквивалентная схема полупроводникового диода, электронных ламп, могут быть инерционными и безынерционными.
1. Безынерционные. 2. Инерционные.

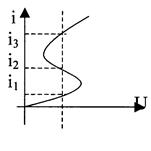
Характеристики НЭ бывают однозначными и многозначными.

|

|
|
Существуют входные, выходные, переходные характеристики. Входная характеристика iб = Ф (Uбэ) , выходная характеристика iк = Ф(Екэ), переходная характеристика iк = Ф (Uбэ)
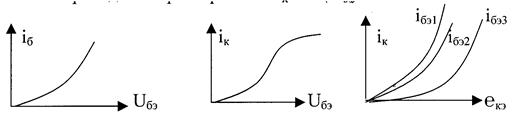
Одной из основных характеристик функциональных узлов является его амплитудная характеристика (АХ).

В некоторых случаях является полезным продуктом преобразование несколько или группы спектральных составляющих тока.

Uвх = Uвх cos  i1 = I1 cos
i1 = I1 cos 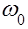 t
t
Scp = I1/Uвх - средняя крутизна
Uвх = I1 Rn ; К = Uвых/ Uвх ; К = Scp Rn ; Scpn = In/Uвх - для п гармоники
Лекция-11
ГРАФИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ОТКЛИКА НЭ НА ВХОДНОЕ ВОЗДЕЙСТВИЕ

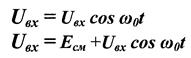
Графический способ определения отклика дает наглядное представление формы сигнала, но не дает возможности определить оптимальный режим работы нелинейного элемента.
Лекция-12 АППРОКСИМАЦИЯ ВАХ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Замена реальных ВАХ НЭ, заданных в виде графиков или таблиц, приближенным аналитическим выражениям, называется аппроксимацией.
Требования, предъявляемые к аппроксимирующей функции:
1. Аппроксимирующая функция должна быть простой.
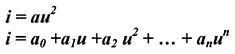
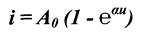
2. Аппроксимирующая функция должна быть такой, чтобы в результате анализа можно было выделить нужные спектральные компоненты тока.

3. Точность аппроксимирующей функции, т.е. насколько точно совпадают значения i и и реальной ВАХ и аппроксимированной.
Наиболее часто в качестве аппроксимирующей функции применяют:
1. полином п ой степени:
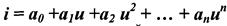
2. полином 2ой степени:
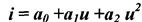
3. укороченный полином 3ей степени.
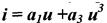
4. Укороченный полином 5ой степени.
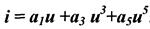
Существует аппроксимация экспонентой i = A∙expau. Аппроксимация суммой экспонент: i = A∙expau+ B expBu+ …
5. Линейно-ломанная аппроксимация (аппроксимация отрезками прямой), если существуют большие уровни входного сигнала.
6. Гиперболический тангенс.

|

Is - ток насыщения; I0 - ток покоя
7. Аппроксимация функцией Крылова.
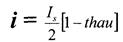
АППРОКСИМАЦИЯ ПОЛИНОМОМ nой СТЕПЕНИ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ АППРОКСИМАЦИИ
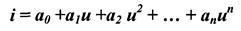
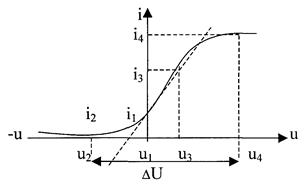
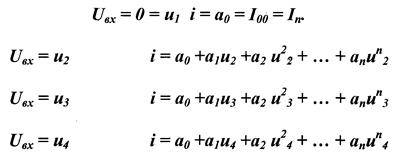
АППРОКСИМАЦИЯ ЭКСПОНЕНТОЙ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ АППРОКСИМАЦИИ

|
Задана ВАХ вакуумного диода

АППРОКСИМАЦИЯ ЛОМАНОЙ ЛИНИИ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ АППРОКСИМАЦИИ
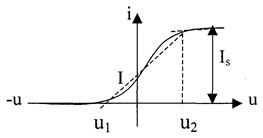
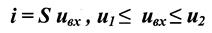

Линейная ломаная аппроксимация применяется при больших уровнях входного сигнала.
Лекция-13
МЕТОДЫ ОПРЕДЕЛЕНИЯ СПЕКТРАЛЬНЫХ СОСТАВЛЯЮЩИХ ТОКА ЧЕРЕЗ НЕЛИНЕЙНЫЙ ЭЛЕМЕНТ

Существуют следующие режимы работы НЭ.
1. Моногармонический режим возбуждения.
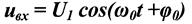
2.Биогармонический режим
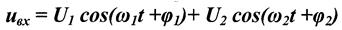
3. Полигармонический режим
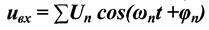
Для ФУ с Нелинейным элементом существует два случая:
Если 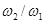 (
( 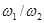 ),можно представить в виде отношения небольших чисел, то такой режим называется синхронным режимом возбуждения.
),можно представить в виде отношения небольших чисел, то такой режим называется синхронным режимом возбуждения.
Если 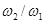 (
( 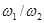 ), не возможно представить в виде отношения небольших чисел, то такой режим называется - асинхронный.
), не возможно представить в виде отношения небольших чисел, то такой режим называется - асинхронный.
В зависимости от выбора аппроксимирующей функции применяют тот или иной метод определения спектральной составляющей (метод спектрального анализа).
1. Аппроксимация полиномом пой степени. i = а0 +a1u +a2 и2 + ... + anun
Используют тригонометрические формулы от кратных аргументов.
2. Аппроксимация ломаной линии: используют метод угла отсечки.
3. Метод трех и пяти ординат, аппроксимация не требуется, спектральные составляющие тока определяются графоаналитическим методом.
4. Аппроксимация экспонентой или сумма экспонент: применяется разложение тока при помощи функции Бесселя от мнимого аргумента.
5. Аппроксимация функцией гиперболического тангенса: разложение в ряд Тейлора.
МЕТОД ПРИМЕНЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФОРМУЛ ОТ КРАТНОГО АРГУМЕНТА.
Этот метод применятся при анализе модуляторов, детекторов, умножителей частоты и т.д.
Рассмотрим действие гармонического сигнала на НЭ, ВАХ которого аппроксимирована полиномом 3ей степени.
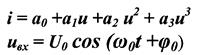
Спектральные составляющие тока.
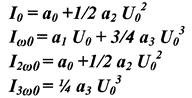
Наивысший номер гармоники равен в степени аппроксимированного полинома.
ДЕЙСТВИЕ ДВУХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ С РАЗЛИЧНЫМИ ЧАСТОТАМИ И НАЧАЛЬНЫМИ ФАЗАМИ
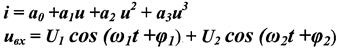
Спектральные составляющие тока.
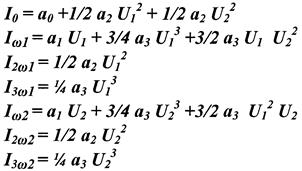
Комбинационные частоты:
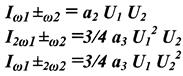
Комбинационные составляющие характеризуются порядком:
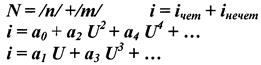
ДЕЙСТВИЕ ДВУХ ГАРМОНИЧЕСКИХ СИГНАЛОВ С КРАТНЫМИ ЧАСТОТАМИ НА НЭ
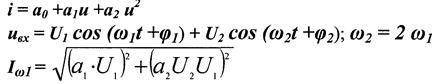
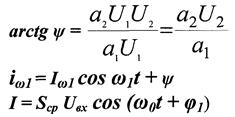
|
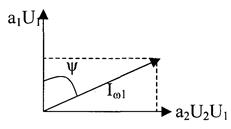
|
Дата добавления: 2021-04-21; просмотров: 533;











