Цифровым фильтром называется линейная частотно-избирательная система, реализуемая на основе вычислительного устройства.

Если n-ый отсчет выходного сигнала фильтра y_n зависит только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1 ..и т.д., то такой фильтр называется нерекурсивным.

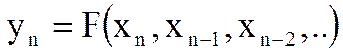
Если n-ый отсчет выходного сигнала фильтра y_n зависит не только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1 ..и т.д., но и от отсчетов выходного сигнала в предшествующие моменты времени, то такой фильтр называется рекурсивным.

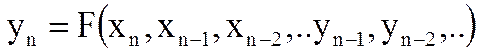
Импульсной характеристикойцифрового фильтра называется выходной сигнал фильтра при действии на его входе единичного отсчета и нулевых начальных условиях.

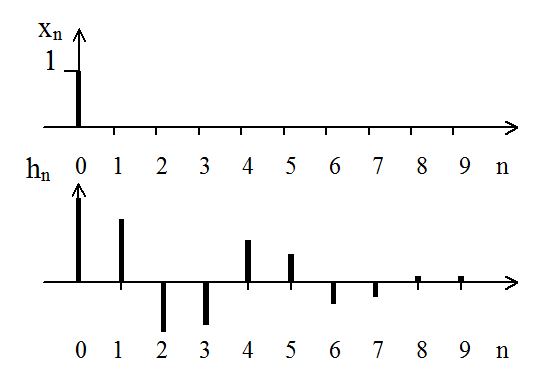
Фильтр с конечной импульсной характеристикой называется КИХ - фильтром (КИХ -конечная импульсная характеристика). Фильтр с бесконечной импульсной характеристикой называют БИХ - фильтром.

2.3. Определение выходного сигнала фильтра по входному сигналу и импульсной характеристике

Определение выходного сигнала цифрового фильтра по входному сигналу и импульсной характеристики основано на определении импульсной характеристики и принадлежности фильтра к линейным системам, для которых справедлив принцип суперпозиции.

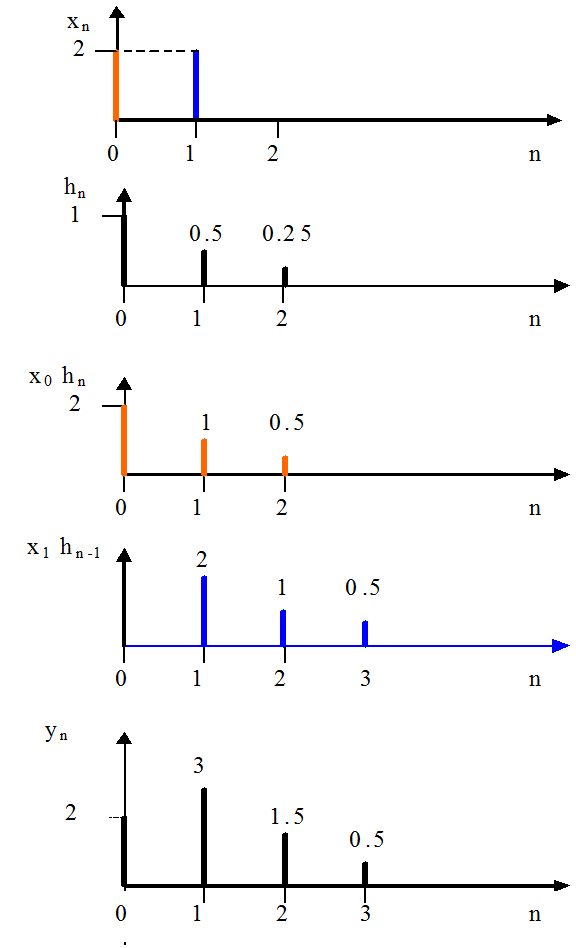
Так как фильтр линейная система, то при входном отсчете в x₀ раз больше единичного, выходной сигнал будет представлять собой импульсную характеристику, все отсчеты которой умножены на x₀, - x₀ h_n.

Определим реакцию фильтра на отсчет сигнала x₁ при x₀ =0. При x₁=1 выходной сигнал фильтра представлял бы собой импульсную характеристику, запаздывающую на один отсчет h_n-1. При отсчете x₁, отличном от единицы, реакцией фильтра будет запаздывающая на один отсчет импульсная характеристика, все отсчеты которой умножены на x₁, - x₁ h_n-1.

Согласно принципу суперпозиции полученные реакции суммируются.

В результате

,

, …..

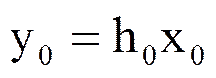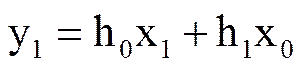В общем случае

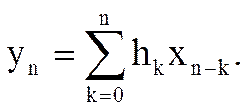(1)

Согласно последнему соотношению

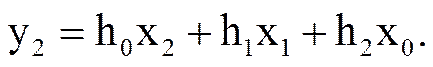
Однако в рассмотренном примере x₂ = 0, поэтому, как видно из рисунка,

В общем случае

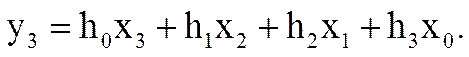
В данном примере x₂ = x₃ = 0, h₃ = 0, поэтому

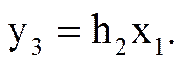
Соотношение (1) представляет собой дискретную свертку последовательностей x_n и h_n, т.е. выходной сигнал фильтра представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра.

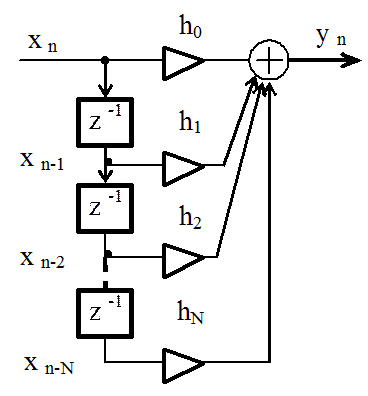
2.4. Системная функция цифрового фильтра. Формы программной реализации фильтра