Сложение синусоидальных функций времени. Векторные диаграммы. Основы символического метода расчета.

Пусть требуется сложить два тока:

;

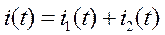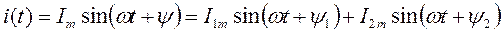(1)

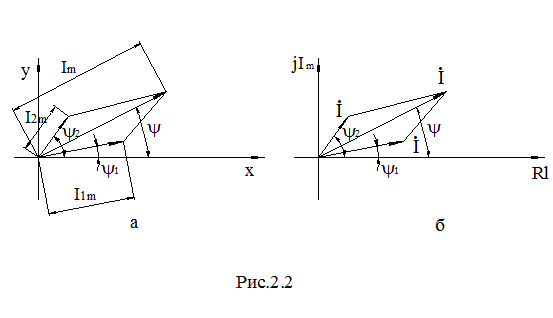
Тригонометрическому уравнению (1) можно дать геометрическую интерпретацию, если каждому синусоидальному значению поставить в соответствие вектор на плоскости в координатах x, y, рис. 2.2а. Длиной вектора будет амплитуда тока, а фазой – начальная фаза синусоиды 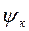. Совокупность векторов, соответствующая уровням токов или напряжений, называется векторной диаграммой.

Уравнению (1) можно поставить в соответствие другое уравнение, в котором каждая синусоида будет представлена в виде комплексного числа.

Ток 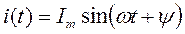можно записать по формуле Эйлера:

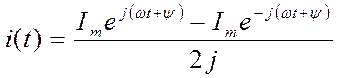(2)

С учетом (2) уравнение (1) примет вид:

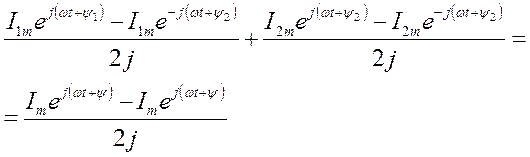(3)

Уравнение (3) содержит два типа комплексных чисел:

Прямые:

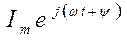
и сопряженные:

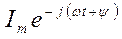
и может быть записано для каждой группы в отдельности, например,

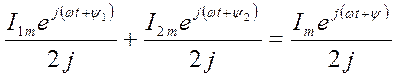(4)

Исключая общие множител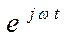и и 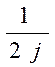, получим:

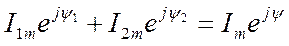(5)

или

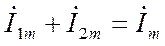
Комплексное число 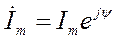называется током в комплексной форме или комплексом тока по максимальному значению. Здесь 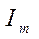- модуль комплекса по максимальному значению, а 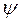- фаза комплекса.

Если за модуль комплекса принять не амплитудное, а действующее значение, то получим комплекс по действующим значениям 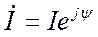или просто комплекс тока.

Уравнение (5) для комплексов тока примет вид:

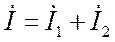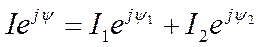или (6)

Геометрическая интерпретация уравнения (6) на комплексной плоскости приведена на рис. 2.2.б. Это так называемая комплексная векторная диаграмма является с учетом масштаба точным аналогом векторной диаграммы, приведенной на рис.2.2.a.

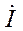Комплекс тока называют символом мгновенного тока i(t), а метод составления уравнений в комплексной форме – комплексным или символическим.

Забегая вперед, отметим, что расчет цепей комплексным методом имеет значительные преимущества перед методом расчета по мгновенным значениям.