ГРАВИТАЦИОННОЕ ОСАЖДЕНИЕ ЧАСТИЦ.

Гравитационное осаждение или седиментация происходит в результате вертикального осаждения частиц под действием силы тяжести при прохождении их через ПУ(рис.3.1. а). При падении частица пыли испытывает сопротивление среды. Наиболее просто это описывается пр прямолинейном и равномерном движении шаровой частицы, то есть в том случае, когда можно пренебречь турбулентностью потока и конвекционными токами:

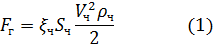
Где 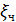- коэффициент лобового сопротивления частицы; S_ч – площадь сечения частиц, перпендикулярного направлению движения, м²; V_ч – скорость движения частицы, м/с; 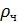– плотность газа кг/м³.

В случае шаровой частицы 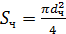; где d_ч – диаметр частицы.

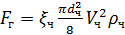(2)

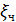зависит критерия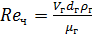

При обычно соблюдаемом в промышленной практике соотношении d_ч >> l_i (где l_i - средняя длина свободного пробега молекулы газа в метрах) сопротивление среды описывается законом Стокса:

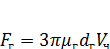(3)

Для частиц размером 0,2-2 мкм в уравнении (3) вводится поправка Кенингема-

Миликена С_к учитывающая повышение подвижности частиц, размер которых сравним со средней длиной свободного пробега газовых молекул l_i:

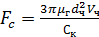С_к = f(l_i; d_ч) (4)

Для воздуха при температуре t_r =20⁰C и Р = 760 мм.рт.ст. l_i =6,5*10⁸м. Существует ряд зависимостей С_к от d_ч .

Закон Стокса применим при ламинарном движении частиц (Re_ч<2).

Для турбулентного режима движения частиц (Re_ч > 500) можно принимать постоянным, равным 0,44.

Для переходного режима (2< Re_ч <500):

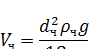
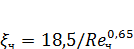
В случае нешарообразных частиц вводится понятие динамического коэффициента формы

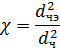
где d_чэ - эквивалентный диаметр частицы, равный диаметру шара, объем кото­рого равен объему данной частицы, м.

В расчетных формулах для определения скорости осаждения час­тиц не шарообразной формы 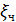заменяется на 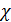, a d_ч на Д_чэ.

Подставляя (3) в (2) получим для области действия закона Стокса:

Форма частиц...................................................... %

Шаровая............................................................... 1

Округленная с неровной поверхностью ………………….2,4

Продолговатая..................................................... 3

Пластинчатая....................................................... 5

Для смешанных тел........................................... 2,9

В общем виде конечная скорость частицы V_ч(м/с), достигается при установлении равновесия между силой сопротивления среды и внешней силой F_b, действующей на частицу:

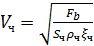; 8

В области действия закона Стокса выражение (8) принимает вид:

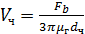(9)

При гравитационном осаждении шаровой частицы:

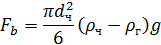
(10)

Подставив выражение (10) в (9) получим V_ч в области действия закона Стокса:

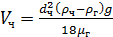(11)

Если пренебречь 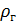то:

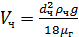(12)

Из формулы (12) следует, что скорость осаждения взвешенных частиц в ПУ, использующих действие силы тяжести, прямо пропорциональна квадрату диаметра частицы.

Скорость падения частицы плотностью р_ч =1000 кг/м³ в неподвижном воздухе.

Диаметр частицы, мкм 100 10 1

Скорость падения, м/с 0,3 0,003 0,00003

Существуют графики зависимости V₄ от d₄ при определенной плотности.

3.2.2. Центробежное осаждение частиц

Этот метод нашел наиболее широкое применение в промышленности (в сухих и мокрых ПУ).

В области существования закона Стокса скорость центробежного осаждения шаровой частицы можно рассчитать, приравнивая центробежную силу F_w развивающуюся при вращении газового потока, стоксовой силе сопротивления среды F_c (рис. 3.1 б).

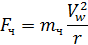
(13)

где V_w- скорость вращения газового потока вокруг неподвижной оси; r - радиус вращения газового потока, м.

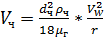(14)

Из выражения (14) следует, что скорость осаждения взвешенных частиц в центробежном ПУ прямо пропорциональна квадрату диаметра частицы. Величина же скорости осаждения при

центробежном осаждении больше, чем при гравитационном в 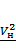раз.

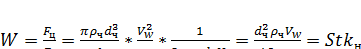(15)

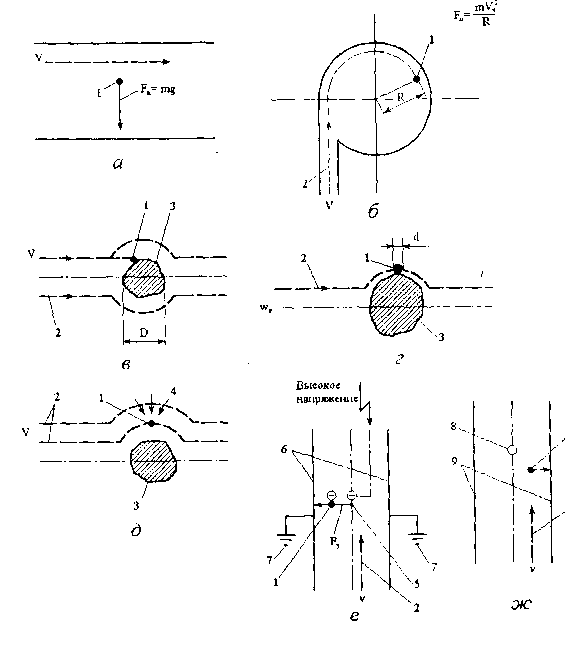Рис. 3.1. Схемы механизмов выделения частиц пыли из газовых потоков: а - под действием силы тяжести; б - под действием центробежных сил; в - инерционное осаждение; г - зацепление; д - диффузионное осаждение; е - электростатическое осаждение; ж - термофорез 1 - частица; 2 - газовый поток; 3 - тело осаждения; 4 - силы диффузии; 5 - электрод корронирующий; 6 - электрод осадительный; 7 - земля; 8 - нагретое тело; 9 - холодная поверхность

Отношение в правой части уравнения (15) есть критерий Стокса. Stk_w, в котором линейный параметр r представляет собой радиус вращения газового потока.

Это позволяет выразить коэффициент осаждения частиц под действием центробежной силы в виде:

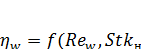
3.2.3. Инерционное осаждение частиц

Инерционное осаждение происходит в том случае, когда масса частицы или скорость ее движения настолько значительны, что она не может двигаться вместе с газом по линии тока, огибающей препятствие, а стремясь по инерции продолжить свое движение, сталкивается с препятствием и осаждается на нем.

При обтекании твердого тела (или капли) запыленным потоком частицы вследствие большой инерции продолжают двигаться поперек изогнутых линий тока газов и осаждаются на поверхности тела (рис. 3.1 в).

Коэффициент эффективности инерционного осаждения, 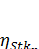, определяется долей частиц, извлеченных из потока при обтекании им тела.

Критерий Стокса является единственным критерием подобия инерционного осаждения. Stk называется «инерционным параметром» и характеризует отношение инерционной силы, действующей на частицу, к силе гидравлического сопротивления среды. Критерий числено равен отношению расстояния, проходимого частицей с начальной скоростью V_ч при отсутствии внешних сил до остановки, к характерному размеру обтекаемого тела (например, диаметру шара).

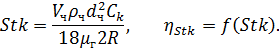
3.2.4. Зацепление

Зацепление (эффект касания) наблюдается, когда расстояние частицы, движущейся с газовым потоком, от обтекаемого тела равно или меньше ее размера (рис. 3.1 г).

Размер частицы играет важное значение при захвате частиц за счет касания частей поверхности обтекаемого тела. Если пренебречь инерционными эффектами и считать, что частица точно следует в соответствии с линиями тока, то частица осаждается не только тогда, когда ее траектория пересечется с поверхностью тела, но и в случае пересечения линии тока на расстоянии от поверхности, равном ее радиусу.

Эффект зацепления характеризуется параметром R, который представляет собой отношение диаметров частицы d_ч и обтекаемого тела d_T.

Эффективность осаждения при зацеплении может быть представлена в виде:

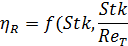
где Re_T критерий Рейнольдса для обтекаемого тела.

Анализ уравнений, описывающих зацепление показывает, что эффект зацепления увеличивается при осаждении частиц на сферах с малым диаметром. Осаждение частиц за счет эффекта зацепления не зависит от скорости газа, но в значительной степени определяется режи­мом течения газового потока.

3.2.5. Диффузионное осаждение

Частицы малых размеров подвержены воздействию броуновского (теплового) движения молекул, в результате которого возможно осаждение этих частиц на поверхности обтекаемых тел или стенок аппарата (рис.3.1 д).

Перемещение частиц в этом случае описывается уравнением Эйнштейна, согласно которому средний квадрат смещения частицы ∆х составляет:

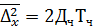
где Д_ч - коэффициент диффузии частицы, характеризующий интенсивность броуновского движения, м²/с.

При справедливости закона Стокса, когда размер частиц больше среднего пути пробега молекул, Д_ч можно выразить как функцию размера частиц:

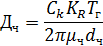
где К_R, - постоянная Больцмана, равная 1,38-10'²³ Дж/К. Для воздуха при Р=760 мм рт.ст. и Т=273 °С. Размер частиц, мкм Коэффициент диффузии, м²/с

Как видно, Д_ч увеличивается с уменьшением размера частиц. Однако скорость диффузии даже субмикронных частиц весьма мала по равнению со скоростью молекул газов, поскольку коэффициент дифузии частиц на несколько порядков меньше. Анализ уравнений показывает, что эффективность диффузионного осаждения обратно пропорциональна размерам частиц и скорости газового потока.

3.2.6. Осаждение под действием электрических зарядов

Электрическая зарядка частиц может быть осуществлена тремя путями: при генерации аэрозоля, за счет диффузии свободных ионов и при коронном разряде. При применении первых двух способов число частиц, получивших положительные и отрицательные заряды, приблизительно одинаково. Коронный разряд, наоборот, приводит к зарядке частиц одним знаком (рис.3.1 е). Зарядка частиц при коронном разряде осуществляется по двум механизмам: воздействием электричекго поля (частицы бомбардируются ионами, движущимися в направлении силовых линий поля) и диффузии ионов. Первый механизм доминирует при размерах частиц более 0,5 мкм, второй - при размерах частиц менее 0,2 мкм. Для частиц диаметром 0,2 - 0,5 мкм эффективны оба механизма, причем минимальная скорость зарядки наблюдается для частиц размером около 0,3 мкм.

Величина заряда q (Кл), приобретаемого под действием электрического поля (I механизм) может быть рассчитана:

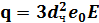
где e₀ - диэлектрическая проницаемость, e₀ = 8,85*10^-12 ф/м; Е - напряженность электрического поля коронного разряда, В/м.

Величина заряда при II (диффузионном) механизме для обычно встречающихся на практике условий.

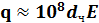
где е - величина заряда электрона, Кл, е= 1,6*10^-19.

Таким образом, максимальная величина q для частиц диаметром

более 0,5 мкм ≈ d², для частиц диаметром менее 0,2 мкм ≈ d_ч.

Электростатическая сила F_E (кулоновская сила), действующая на заряженную частицу в электрическом поле напряженностью Е:

F_E=qE.

В области применения закона Стокса V_ч можно рассчитать, приравнивая F_E стоксовой силе F_с :

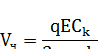
На методе электрического осаждения частиц основана работа электрофильтров. Кроме того, электрические силы могут оказывать влияние на осаждение частиц и в мокрых ПУ, где наблюдаются различные электрические силы.

3.2.7. Термофорез

Термофорез представляет собой отталкивание частиц нагретыми телами, вызванное силами, действующими со стороны газообразной фазы на находящиеся в ней неравномерно нагретые частицы аэрозоля (рис. 3.1 ж). Механизм этих сил существенно зависит от отношения размера частицы и средней длины свободного пробега газовых молекул.

При d_ч << l_i термофоретическая сила F_T, действующая на частицу, определяется:

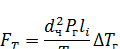
где Р_r - абсолютное давления газов, Па; ∆Т_г - градиент температуры в газах, К/м.

Так как P_гl_i = const, то F_T ≈ 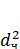и не зависит от давления.

Явление термофореза, наблюдаемое в аэрозолях, называется термопреципитацией. Это явление играет существенную роль при улавливании частиц из горячих газов в случае их прохождения через холодные насадки. В узких каналах при разнице температур 50°С можно по­лучить температурный градиент 1000К/см. Расчеты показывают, что это должно привести к осаждению на 98,8% частиц размером 0,1мк в слое насадки глубиной 230мм при 500°С.

Представляет интерес зависимость скорости термофореза от температуры. Когда размер частиц больше 1 мкм, отношение скорости термопреципитации к тепловому градиенту увеличивается с температурой, в то время как для частиц размером менее 1мкм оно уменьшается.

Явление термофореза приводит и к отрицательным результатам. Так, твердые частицы, оседающие из горячих газов на холодных стенках котлов и теплообменников образуют слой с низкой теплопроводностью, что приводит к значительному снижению коэффициента тепло­передачи.

.

Диффузиофорез

Диффузиофорез - движение частиц, вызываемое градиентом концентрации компонентов газовой смеси. Это явление отчетливо проявляется в процессах испарения и конденсации.

При испарении с поверхности капли (или пленки жидкости) возникает градиент концентрации пара, но так как общее давление пара должно оставаться постоянным, происходит гидродинамическое течение парогазовой смеси (ПГС), направленное перпендикулярно к по­верхности испаряющейся капли и компенсирующее диффузию газов к этой поверхности.

Это гидродинамическое движение называется стефановским и может оказывать существенное влияние на осаждение частиц. Так, при улавливании частиц распыленной водой при недосыщении газов водяным паром стефановское течение препятствует, а при перенасыщении - способствует захвату частиц каплями.

Математическое выражение рассмотренного явления носит название закона Стефана и при конденсации паров имеет вид:

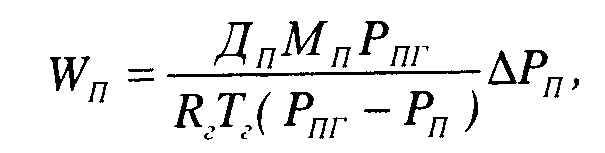
где W_П - количество вещества, продиффундирующего за 1с через 1 м2 поверхности, кг/м2с; Рт- давление ПГС. Па; Рп - парциальное давление пара, Па; ДЦ- коэффициент диффузии пара, м2/с; Мп - масса 1 кмоль пара, кг/моль; ДРп - изменение парциального давления пара по оси, нормальной к поверхности капли - градиент парциального давления пара, Па/м.

Уравнение Стефана справедливо и при испарении, в этом случае в правой части уравнения появляется знак минус.