Модальное управление с запаздыванием

Предположим теперь, что быстродействие ЦВ не велико, так что время 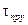на преобразование сигналов и расчет управления, сравнимо с периодом квантования, и удовлетворяет условию (16.3). В этом случае запаздыванием пренебречь нельзя и модальное управление берется в следующей форме:

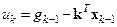. (16.14)

Здесь для вычисления значения управления, соответствующего моменту времени 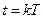, используются данные, полученные в 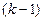-м такте. Поэтому уравнение замкнутой системы (16.4), (16.14), очевидно, имеет вид

.

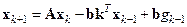Запишем это уравнение в z-изображениях при нулевых начальных условиях, т.е. при 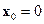. В результате получим

.

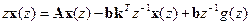Умножим обе части этого равенства на z и приведём подобные. Тогда будем иметь

.

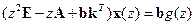Снова используя указанное выше свойство определителей, заключаем, что в данном случае характеристический полином замкнутой системы определяется выражением

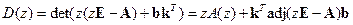. (16.15)

Отсюда следует, что при наличии запаздывания в ЦУУ на один такт степень характеристического полинома замкнутой системы становится равной n + 1, а число варьируемых коэффициентов модального управления с запаздыванием (16.14), по-прежнему, n. Следовательно, для обеспечения произвольного расположения всех корней характеристического полинома системы в управлении (16.14) не хватает одного коэффициента.

Поэтому при использовании управления (16.14) (т.е. дискретного модального управления с запаздыванием на один такт) можно обеспечить только такое расположение корней характеристического полинома (16.15) замкнутой системы, при котором один из коэффициентов её желаемого полинома равен соответствующему коэффициенту характеристического полинома (16.10) объекта управления, заданного дискретной моделью (16.4).

Рассмотрим расчет коэффициентов k_i в управлении (16.14) на следующем примере.

Пример 16.2. Предположим объект управления тот же, что и в предыдущем примере, т.е. описывается уравнениями (16.13). Найти одно из возможных дискретных модальных управлений с запаздыванием на такт, при котором обеспечивается устойчивость замкнутой системы.

Решение. В данном случае n = 2, поэтому в соответствии с выражением (16.14) дискретное управление

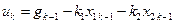. (16.16)

При этом характеристический полином замкнутой системы (16.13), (16.16), согласно (16.15), с учетом того, что 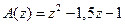, равен

.

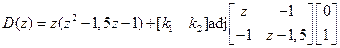Так как 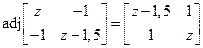, то из предыдущего выражения, находим

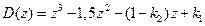. (16.17)

Таким образом, корни характеристического полинома замкнутой системы нужно задать так, чтобы их сумма равнялась 1,5. При этом для обеспечения устойчивости замкнутой системы модуль каждого из них, в соответствии с условием (15.48), должен быть меньше единицы. В данном случае корни можно задать, например, так 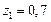; ; 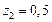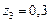. Тогда желаемый полином

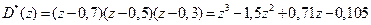. (16.18)

Сравнивая полиномы 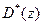(16.18) и 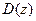(16.17), находим 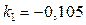; 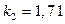. Следовательно, искомое дискретное модальное управление с запаздыванием на такт имеет вид .

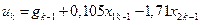Как и выше, для проверки полученного результата подставим найденное управление в уравнение объекта (16.13). В результате получим

.

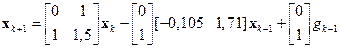Перейдя в этом выражении к z-изображениям, найдём, что характеристическое уравнение синтезированной замкнутой системы определяется выражением

.

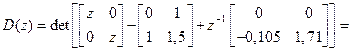
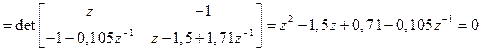Следовательно, характеристический полином синтезированной системы управления равен 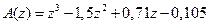. Сравнивая полученный полином с выражением (16.18), заключаем, что синтезированная дискретная система имеет заданные при её синтезе корни характеристического уравнения.

На основе изложенного можно заключить, что в случае дискретного модального управления с запаздыванием на такт не всегда можно обеспечить заранее заданное расположение полюсов дискретной системы, если даже объект вполне управляемый. Действительно, если в рассматриваемом случае коэффициент 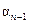характеристического полинома (16.10) заданного объекта (16.4) не равен сумме n чисел по модулю меньших единицы, то задача определения коэффициентов модального управления (16.14), очевидно, не имеет решения. В этих случаях для построения модального дискретного управления необходимо более точно учитывать запаздывание, вносимое АЦП, ЦВ и ЦАП, непосредственно при выводе уравнений дискретной модели объекта управления.

Отметим также, что при синтезе астатических дискретных систем с модальным управлением выбор желаемых корней характеристического полинома должен удовлетворять дополнительному условию астатизма заданного порядка дискретных систем управления (см. § 15.8).

В целом же можно заключить, что модальное дискретное управление при определенных условиях позволяет обеспечить желаемое расположение полюсов дискретных САУ, но предполагает доступность прямому измерению всех переменных состояния системы. При этом для получения приемлемого качества процесса управления необходимо выбирать желаемые значения полюсов так, чтобы переходный процесс системы был близок к желаемому. Как правило, это требует нескольких итераций. В этом смысле рассматриваемый далее метод синтеза дискретных систем по желаемым показателям качества является более рациональным, тем более что он не требует измерения переменных состояния.