Остаются неподвижными.

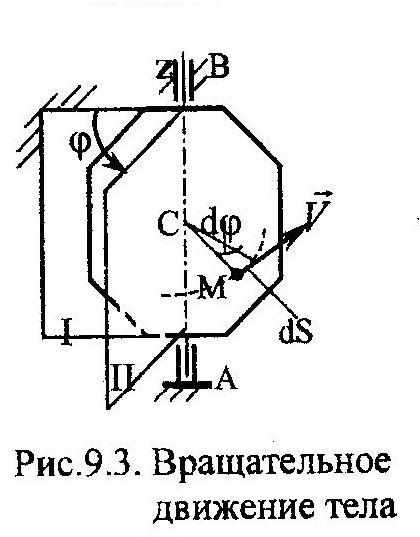
На рис. 9.3 видно, что положение тела при его вращательном движении можно определить

с помощью угловой координаты,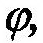

которая откладывается от неподвижной плоскости

I к подвижной плоскости II, жестко связанной с телом.

Однозначная зависимость угловой координаты от времени является уравнением враща-тельного движения:

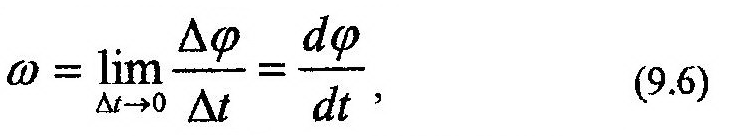Основными кинематическими характеристиками вращательного движения тела являются его: угловая скорость – величина, характеризующая изменение угловой координаты и угловое ускорение – величина, определяющая изменение угловой скорости

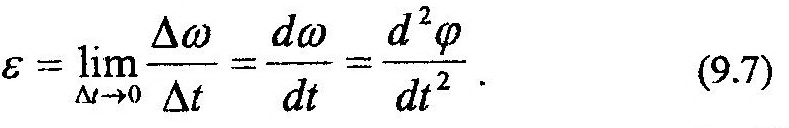
По формулам (9.6) и (9.7) видно, что определить эти кинематические характеристики тела можно как пределы отношений соответствующих приращений. Выражение для скорости какой-либо точки М тела (рис. 9.3) можно получить из формулы (8.6):

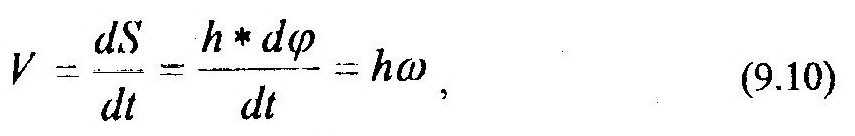
где h – кратчайшее расстояние от точки М до оси вращения.

Выражение для касательной, a_r, и нормальной, a_n, составляющих ускорения точки М могут быть найдены с помощью формул системы (8.8):

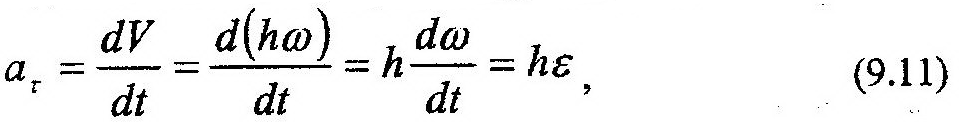
и

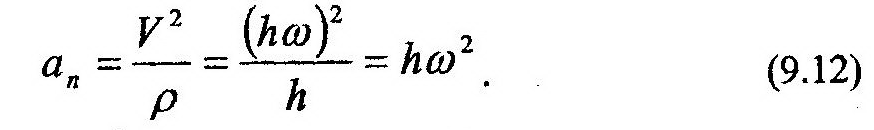
ЛЕКЦИЯ 8. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

<9 10 111213 14 15 >

Дата добавления: 2016-12-16; просмотров: 1227;

Поиск по сайту