Классический ПИД-регулятор

Автоматические регуляторы (АР) реализуют типичные законы регулирования: пропорциональный (П), пропорционально-интегральный (ПИ), пропорционально-дифференциальный (ПД), пропорционально-интегрально-диференциальный (ПИД). Эти законы определяются функциональной зависимостью выходного и входного сигналов автоматического регулятора (основной областью применения АР являются локальные и автономные системы контроля и регулирования).

Главная функция регулятора – формирование сигнала рассогласования (или ошибки) между регулируемой величиной и ее заданным значением (установкой), а также динамическое преобразование сигнала рассогласования по типовым алгоритмам (законам) регулирования. Управляющий сигнал с выхода регулятора поступает непосредственно на вход исполнительного устройства автоматической системы, связанного с объектом управления. Типичное включение АР в систему автоматического управления представлено на рис. 15.1.

К современным АР предъявляются дополнительные эксплуатационные требования, а именно:

· гальваническое разделение входных и выходных цепей;

· связь с УВМ верхнего уровня иерархии управления;

· аналоговая или дискретная автоподстройка динамических параметров регулятора, необходимая для построения адаптивных систем управления;

· ограничения выходного аналогового сигнала по верхнему и нижнему уровням и сигнализации предельных значений этих уровней.

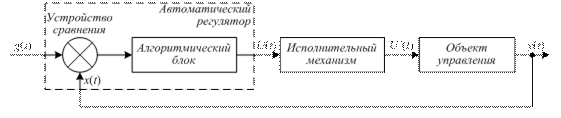
g(t) – сигнал установки;

y(t) – регулируемая величина;

x(t) – сигнал ошибки;

U(t), U’(t) – сигналы, которые непосредственно присутствуют на выходе регулятора и исполнительного механизма

Рисунок 15.1 – Стандартное включение автоматического регулятора в систему автоматического управления

Автоматические регуляторы можно классифицировать по нескольким признакам. В зависимости от электрического сигнала АР делятся на аналоговые, дискретные и аналого-дискретные (гибридные). В свою очередь, дискретные регуляторы могут быть импульсными и цифровыми. В аналоговых регуляторах информационный сигнал непрерывный во временном отрезке формирования сигнала регулирования. В дискретных регуляторах в одной или нескольких точках временного отрезка формирований регулирующего сигнала происходит либо импульсная модуляция сигнала, либо операция с кодами. В гибридных регуляторах информационные сигналы представлены как в аналоговой, так и в дискретной форме.

Математическую модель ПИД-регулятора можно записать в следующем виде:

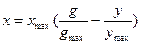(15.1)

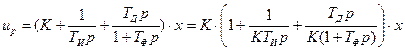(15.2)

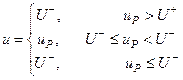, (15.3)

где 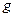, 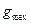– соответственно входное воздействие и его максимальное значение;

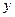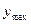, – соответственно управляемая величина и ее максимальное значение;

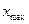– максимальный сигнал-ошибка;

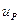- сигнал, который формируется в соответствии с ПИД-законом регулирования;

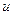- выходной сигнал ПИД-регулятора, который учитывает наложенные ограничения;

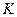- коэффициент усиления пропорциональной составляющей регулятора;

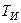- постоянная времени интегрирования (время изодрома) для интегрирующей составляющей регулятора;

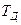- постоянная времени дифференцирования (время передачи) для дифференцирующей составляющей регулятора;

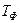- постоянная времени фильтрации, которая обеспечивает приведение характеристик дифференцирующей составляющей к реальному виду;

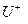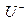, - соответственно верхняя и нижняя границы заданных ограничений входного сигнала.

Структурная схема ПИД-регулятора в соответствии с (15.1) – (15.3), представлена на рис. 15.2.

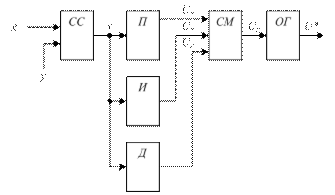
Рисунок 15.2 – Структурная схема ПИД-регулятора

Блок СС в структурной схеме выполняет роль суммирующего (сравнивающего) устройства и служит для формирования сигнала рассогласования (ошибки) x в соответствии с выражением (15.1).

Структурная схема регулятора содержит три параллельных ветви, которые реализуют каждая соответственно пропорциональную, интегральную и дифференциальную составляющие закона регулирования. Эти составляющие ПИД-закона регулирования представлены соответственно первым, вторым и третьим членом в круглых скобках в (15.2). Т.е., в структурную схему ПИД-регулятора входят три параллельно включенных блока, которые реализуют коэффициент усиления 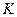, интегральную 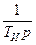и инерционно-дифференциальную 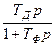составляющие закона регулирования. Сигналы трех параллельных ветвей суммируются в соответствии с 15.2 на сумматоре СМ. Ограничение выходного сигнала ПИД-регулятора обеспечивается включением в его состав ограничителя ОГ, который реализует (15.3).

Амплитудно-частотная и фазо-частотная характеристики передаточной функции (15.2) при параметрах 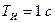, , 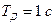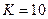показаны на рис. 15.3.

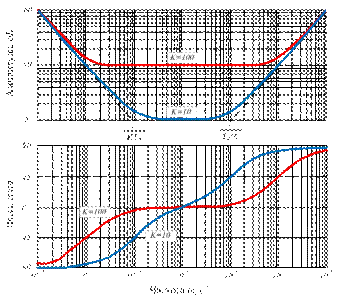
Рисунок 15.3 – АЧХ и ФЧХ ПИД-регулятора при 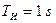, , 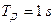, 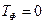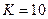и

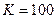
Переходная характеристика ПИД-регулятора (реакция на единичный скачок) представляет собой сумму постоянной составляющей 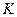, прямой линии 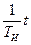, полученной при интегрировании единичного скачка и дельта-функции Дирака 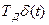, полученной при дифференцировании единичного скачка.

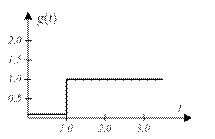
Рисунок 15.4 а – Входной сигнал ПИД-регулятора

При подаче на вход регулятора единичного скачка (функция Хевисайда), реакция на выходе пропорциональной составляющей повторяет входной сигнал (при К = 1) либо увеличивает высоту «ступеньки» в два раза (при К = 2).

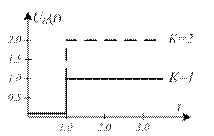
Рисунок 15.4 б – Реакция П-звена

Реакция на выходе интегрирующей составляющей – линейно растущий сигнал, который за время t = 1 s достигает значения 1 V (при Т_И = 1) либо 0,5 V (при Т_И = 2).

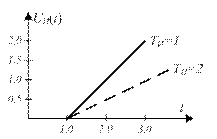
Рисунок 15.4 в – Реакция И-звена

Реакция дифференцирующей составляющей ПИД-регулятора на единичный скачок – единичный импульс (функция Дирака) (при Т_Ф = 0). В случае реального дифференцирующего звена (Т_Ф > 0) выходной сигнал имеет затянутый задний фронт.

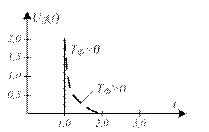
Рисунок 15.4 г – Реакция Д-звена

Выходной сигнал регулятора является суммой реакций параллельно включенных П, И и Д-звеньев.

Рисунок 15.4 д – Реакция ПИД-регулятора

На рис. 15.5 показан пример реакции замкнутой системы автоматического управления для объекта второго порядка. Уменьшение амплитуды колебаний и увеличение коэффициента затухания с ростом постоянной дифференцирования 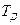объясняется тем, что благодаря положительному наклону АЧХ в области 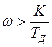(см. рис. 15.3) уменьшается сдвиг фаз в контуре регулирования. Дальнейшее увеличение постоянной дифференцирования (т.е. снижение частоты 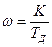) приводит к росту усиления ПИД-регулятора на высоких частотах, при 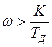(рис. 15.3).

При увеличении фазового сдвига, связанного с транспортной задержкой, с ростом частоты и увеличении усиления в связи с ростом 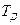всегда наступает момент, когда петлевое усиление системы на частоте фазового сдвига 180⁰ превысит единицу. При этом на переходной характеристике замкнутой системы сначала появляются затухающие колебания (кривая 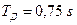), затем, при дальнейшем уменьшении 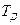, система переходит в колебательный режим.

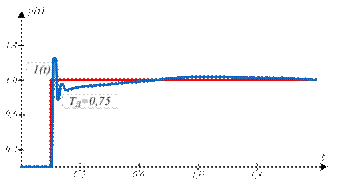
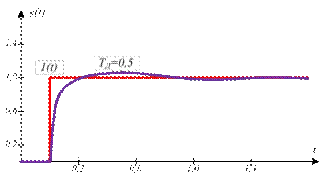
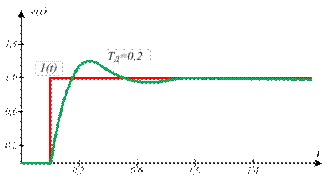
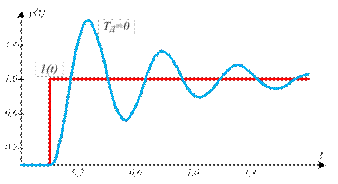
Рисунок 15.5 – Реакция замкнутой системы с ПИД регулятором на единичный скачок при 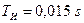, 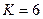для объекта вида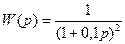

Детальный анализ работы ПИД-регуляторов приведен, в частности, в «Энциклопедия АСУ ТП» (Google), [18] и др.

Несмотря на долгую историю развития и большое количество публикаций, посвященных ПИД-регуляторам, остается много проблем в таких вопросах как устранение интегрального насыщения при регулировании в контурах с гистерезисом, при управлении нелинейными объектами и объектами с транспортной задержкой. Практические реализации ПИД-контроллеров не всегда содержат антиалиасные фильтры, граничная частота фильтра часто выбрана неправильно, чрезмерный шум и внешние возмущения затрудняют настройку параметров. Проблемы усложняются тем, что в современных системах управления динамика часто неизвестна, регулируемые процессы нельзя считать независимыми, измерения сильно зашумлены, нагрузка непостоянна, технологические процессы непрерывны.

Часть проблем возникает по причине сложности эксплуатации. Во многих ПИД-контроллерах дифференциальная компонента выключена только потому, что ее трудно правильно настроить. Пользователи пренебрегают процедурой калибровки, недостаточно глубокие знания динамики регулируемого процесса не позволяют правильно выбрать параметры регулятора. В результате до 30 % регуляторов, используемых в промышленности, настроены неправильно. Поэтому основные усилия исследователей в настоящее время сосредоточены на поиске надежных методов автоматической настройки регуляторов, как встроенных в ПИД контроллер, так и функционирующих на отдельном компьютере [18].

На отечественном рынке ПИД-контроллеры наиболее хорошо представлены продукцией фирм ABB, Foxboro, Honeywell, Yokogawa, Toshiba, Siemens, Omron, Контравт, Овен, НИЛ АП.

СПИСОК ЛИТЕРАТУРЫ

1. Воробьев М.И. Проектирование электронных устройств. – М.: Высш.шк., I989. – 233 с.

2. Попов Э.П. Теория линейных систем автоматического управления и регулирования. – М.: Наука,1978. – 255 с.

3. Теория автоматического управления / Под общ. ред. А.В. Нетушила. - М.: Высш. шк., 1968. – ч. 1. – 423 с.

4. Сборник задач по теории автоматического регулирования и управления / Под ред. В.А. Бесекерского. – М.: Наука, 1978. – 510 с.

5. Прагер И.Л. Электронные аналоговые вычислительные машины. – М.: Машиностроение, 1979. – 230 с.

6. Шило В.Л. Линейные интегральные схемы. – М.: Сов. радио, 1979. – 866 с.

7. Гальперин M.В. Практическая схемотехника в промышленной автоматике. – М.: Энергоиздат, 1987 – 319 с.

8. Алексеенко А.Г., Коломбет В.А., Стародуб Т.Н. Использование прецизионных аналоговых микросхем. – М: Радио и связь, I985. – 304 с.

9. Попов Б.Ф. Теория линейных систем автоматического управления и регулирования. – М.: Наука, 1978. – 255 с.

10. Скаржепа В.А., Луценко А.Н. Электроника и микросхемотехника. – Киев: Высшая шк., 1989. – 430 с.

11. Федорков Б.Г., Телец В.А. Микросхемы ЦАП и АЦП: функционирование, параметры, применение. – М.: Энергоатомиздат, 1990. – 318 с.

12. Микроэлектронные цифроаналоговые и аналого-цифровые преобразователи информации / Под ред. Смолова В.Б. – Л.: Энергоиздат, I976. – 335 с.

13. Горбацевич В.Д., Левинзон Ф.Ф. Аналоговое моделирование систем управления – М.: Наука, 1984. – 301 с.

14. Тихванов Р.И. Операционные блоки автоматических вычислительных устройств. – Л.: Энергоиздат, I989. – 208 с.

15. Сопряжение датчиков и устройств ввода данных с компьютерами IBM PC: Пер. с англ./Под ред. У. Томпкинса, Дж. Уэбстера. – М.: Мир, 1992. – 592 с., ил.

16. Малахов В.П. Схемотехника аналоговых устройств: Учебник. – Одесса: Астропринт, 2000. – 212 с.

17. Методы практического конструирования при нормировании сигналов c датчиков: Пер. с англ. Горшкова Б. Л. – М.: ЗАО АВТЕКС, 2000. – 311 с.

18. Денисенко В.В. Компьютерное управление технологическим процессом, экспериментом, оборудованием – М.: Горячая линия-Телеком, 2009. – 608 с.

19. ГОСТ 8.417-2002. Единицы величин. – Все таблицы и правила перевода, SI (С)

20. Единицы величин: Словарь-справочник. — Москва, Издательство стандартов, 1990, ISBN 5-7050-0118-5

21. Источник - Материал из Википедии, свободной энциклопедии

22. Таблица названий, обозначений и единиц измерения физических величин