Генерация ключей в RSA

1. Выбираем два взаимнопростых фактора p и q. Например: p = 3, q = 11 p ¹ q;

2. Вычисляем модуль RSA. n = pq (mod RSA = p*q = 33);

3. Вычисляем функцию Эйлера m = (p – 1)(q – 1). (m = (3 – 1)(11 – 1) = 20);

4. Выбираем фактор d < n – простое число (d = 7);

5. Из модульного уравнения d*e = 1modm вычисляем фактор e. Преобразуем:

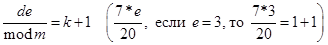
6. Составляем секретный и открытый ключи RSA.

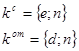У нас: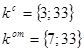

7. Для сохранения (обеспечения) секретности ключей необходимо «убрать мусор», уничтожить p, q, m.

а) Шифрование: 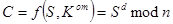– по modn вычислить остаток;

б) Дешифрование: – вычислить остаток по modn.

При этом сообщение S и шифротекст С не должен превосходить модуль RSA n

(S,C) £ n

Сообщение S и шифротекст С сворачиваются в целое число.

Свёртка: S = АДА

Исходник записывается в форме полинома с основанием равным длине алфавита А = {А,Б,В,...,Я} – 32 символа.

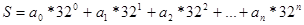, где n – длина сообщения.

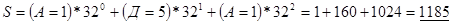
Развёртка: 1185 32

96 37 32

225 32 1 = А

224 5 = Д

1 = А

Шифрование: Исходник S = 1185

Так как сообщение S превышает модуль RSA n = 33, то сообщение S разбивают на блоки, и каждый блок шифруется самостоятельно S = 1185 > n = 33

Дешифрование:

Криптостойкость RSA:

1. Сверхвысокая криптостойкость, ключи не взламываются;
2. Ключи долговременные, постоянные;
3. Не нужен закрытый канал связи, т.к. секретный ключ не передается.

Недостаток: системы работают медленно, т.к. идет большая вычислительная работа (возведение больших целых чисел в большую целую степень).