Погрешности средств измерений

Точность СИ – это качество, характеризующее близость показываемого (измеренного) значения к истинному значению.

Численно точность оценивается через погрешность.

Погрешность СИ – разность между показанием СИ (измеренным значением) и истинным (действительным) значением измеряемой величины.

Погрешности СИ делятся на:

· в зависимости от условий возникновения – основные и дополнительные;

· в зависимости от изменения во времени измеряемой величины – статические и динамические;

· в зависимости от значения измеряемой величины – аддитивные и мультипликативные;

· по закономерности проявления – систематические и случайные.

Погрешность СИ можно численно выразить как абсолютную, относительную, приведенную.

Действительное значение – значение физической величины, полученное экспериментально и настолько близкое к истинному значению, что может быть использовано вместо него. Действительное значение может быть получено по показанию эталонного прибора (погрешность эталонного прибора должна быть значительно меньше погрешности прибора, с помощью которого определено значение Х).

Влияющая величина – любая величина, обычно внешняя по отношению к измерительному прибору, которая может оказать влияние на его метрологические характеристики.

Нормальные условия –совокупность установленных значений и установленных областей значений влияющих величин, при которых нормируются допускаемые основные погрешности прибора.

Рабочая область применения – заданная область значений, которые может принимать влияющая величина, не вызывая изменений показаний, превышающих установленное значение.

Основная погрешность – погрешность СИ, при его применении в нормальных для него условиях (температура, влажность, напряжение питания и др.). Значение основной погрешности нормируется и указывается в технической документации на СИ.

Дополнительная погрешность – составляющая погрешности СИ, возникающая дополнительно к основной погрешности при его применении в условиях, когда хотя бы одна из влияющих величин выходит за установленные границы. Значение дополнительной погрешности нормируется и указывается в технической документации на СИ.

Статическая погрешность – погрешность СИ, применяемого при измерении физической величины, принимаемой за неизменную во время измерений.

Динамическая погрешность – погрешность СИ, возникающая при измерении изменяющейся во времени физической величины.

Аддитивная погрешность – составляющая погрешности СИ, остающаяся постоянной во всем диапазоне измерений (не зависит от размера измеряемой величины).

Мультипликативная погрешность– составляющая погрешности СИ, линейно зависящая от значения измеряемой величины X (погрешность растет с увеличением X).

Систематическая погрешность – составляющая погрешности СИ, которая остается постоянной или закономерно изменяется. К систематическим погрешностям относят погрешности градуировки шкалы, погрешности, обусловленные неточностью меры и т.п.

Случайная погрешность – составляющая погрешности СИ, изменяющаяся случайным образом. Случайные погрешности вызываются большим числом отдельных (в том чисел и неизвестных) причин, действующих независимо друг от друга, поэтому нельзя заранее предвидеть их появление и исключить опытным путем.

Значение случайной погрешности можно определить с помощью статической обработки результатов многократных равноточных (с одинаковой точностью) измерений.

Абсолютная погрешность – погрешность СИ, выраженная в единицах измеряемой величины.

Абсолютная погрешность D есть разность между показанием прибора X и истинным (действительным) значением X_Д измеряемой величины:

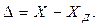(1.3)

Поправка – абсолютная погрешность, взятая с обратным знаком. При сложении поправки с показанием прибора X получается действительное значение X_Д.

Относительная погрешность d - погрешность СИ, выраженная отношением абсолютной погрешности D СИ к результату измерений Х или к действительному значению X_Д измеряемой величины. Выражается в процентах.

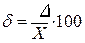или 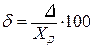. (1.4)

Приведенная погрешность 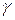- погрешность СИ, выраженная отношением абсолютной погрешности СИ к нормирующему значению X_Н. Выражается в процентах.

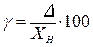. (1.5)

За нормирующее значение у вольтметров и амперметров принимается их верхний предел измерения.

Приведенная погрешность у приборов с резконеравномерной шкалой, в том числе у электромеханических омметров, рассчитывается по формуле

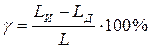(1.6)

где L – длина всей шкалы омметра, мм;

L_И – длина части шкалы от крайней левой отметки до положения стрелки прибора при измерении, мм;

L_Д – длина части шкалы от крайней левой отметки до положения стрелки, которое она бы занимала, показывая действительное значение, мм.

Длина шкалы L указывается в паспорте прибора, но ее и две другие длины можно измерить линейкой.

Рассмотрим пример.

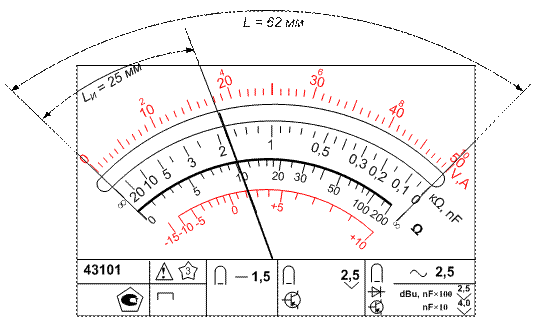
При поверке тестера 43101 по шкале «W» (рис. 1.4) проведено измерение сопротивления резистора, действительное значение которого R_Д, определенное с помощью эталонного прибора, равно 9,5 Ом. Стрелка поверяемого тестера отклонилась при измерении на 25 мм, что соответствует R_и = 10 Ом.

С помощью линейки определяем L = 62 мм, L_Д = 23,5 мм и вычисляем .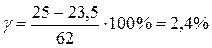

Класс точности СИ – обобщенная характеристика, отражающая уровень точности СИ, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.

Класс точности может выражаться одним числом или двумя числами (в виде их отношения).

Рис. 1.4. Расчет приведенной погрешности измерения сопротивления тестером 43101 по шкале «Ω» (выделена жирно)

Если мультипликативная составляющая погрешности отсутствует (или b·X << a), абсолютная погрешность прибора оказывается постоянной в любой точке шкалы: Δ_max = ± a. В этом случае класс точности К выражается одним числом, в процентах, т.е.

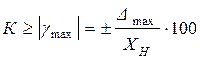, (1.7)

где Х_Н – нормирующее значение.

Класс точности устанавливается из стандартного ряда. Это ближайшее к 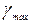большее ее число.

К приборам, у которых класс точности выражается одним числом, относятся электромеханические аналоговые (стрелочные) и самопишущие приборы. Для электромеханических амперметров и вольтметров установлены следующие классы точности: 0,05; 0,1; 0,2; 0,3; 0,5; 1,0; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0.

Зная класс точности, можно рассчитать пределы допускаемой относительной погрешности измерений (в процентах) для любого показания амперметра или вольтметра по формуле:

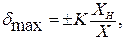(1.8)

где K – класс точности (обозначен на циферблате прибора);

Х_Н – нормирующее значение, равное пределу измерений;

X – измеренное значение (показание прибора).

У аналоговых приборов с резконеравномерной шкалой, в том числе у омметров, класс точности K также выражается одним числом и записывается на циферблате прибора в виде числа с подчеркиванием, например, (см. рис. 1.4 и особенности расчета приведенной погрешности для таких приборов).

Класс точности здесь также означает, что максимальная приведенная погрешность не должна превышать его значение (K ³g_max). Для аналоговых омметров установлены следующие классы точности: 0,05; 0,1; 0,2; 0,5; 1; 1,5; 2; 2,5; 3; 5; 10; 20.

Пределы допускаемой относительной погрешности d_Rmax измерения сопротивления омметром рассчитываются по формуле:

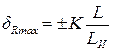, (1.9)

где K, L_И и L – см. (1.6) и рис. 1.4.

Если аддитивная и мультипликативная составляющие основной абсолютной погрешности соизмеримы (близки по значениям друг к другу), то абсолютная погрешность 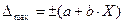и класс точности обозначается в виде отношения двух чисел c/d, например, класс точности 0,1/0,05. Коэффициент «с» определяет аддитивную погрешность, а «d» – мультипликативную.

В этом случае предельное значение основной относительной погрешности (в процентах) определяется по формуле:

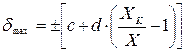, (1.10)

где X_К - конечное значение выбранного диапазона измерений;

X – измеренное значение.

К приборам, класс точности которых выражается двумя числами, относятся цифровые приборы, а так же измерительные мосты и компенсаторы.

Вариация показаний – разность между показаниями ИП, соответствующими одному и тому же действительному значению измеряемой величины при двух направлениях медленных изменений значения измеряемой величины в процессе подхода к данной точке диапазона измерений (первый раз - приближением снизу шкалы, второй раз – приближением сверху).

Предел допускаемой вариации показаний не должен превышать предела допускаемой основной погрешности.