Метод Гиллеспи (метод отталкивания электронных пар валентной оболочки)

Этот метод основан на том, что реальная геометрия молекулы определяется не только гибридизацией АО, но и числом двухэлектронных двухцентровых связей (связывающих электронных пар) и наличием неподеленных электронных пар (Е). Тогда при одинаковой гибридизации молекула метана соответствует формуле CH₄, аммиака – NH₃E, воды – H₂OE₂. При этом каждая молекула представляет собой геометрическую фигуру, вписанную в сферу. Молекула будет иметь минимум энергии, если все связывающие электронные пары будут равноудалены друг от друга на поверхности сферы. Неподеленная электронная пара занимает на сфере большую площадь, что приводит к уменьшению валентного угла тем больше, чем больше в молекуле неподеленных электронных пар E.

Основные положения метода.

1. Геометрия молекулы или иона определяется исключительно числом электронных пар на валентной оболочке центрального атома.

2. Электронные пары принимают такое расположение на валентной оболочке атома, при котором они максимально удалены друг от друга, т.е. электронные пары ведут себя так, как если бы они взаимно отталкивались.

3. Область пространства, которую занимает несвязывающая неподеленная пара электронов, имеет большие размеры, чем та область, которая занята связывающей электронной парой. Отталкивание между электронами несвязывающей неподеленной пары центрального атома и связывающей пары сильнее, чем между электронами связывающих пар.

4. Две электронные пары двойной связи занимают большую область пространства, чем одна электронная пара простой связи.

Обозначения, используемые для описания геометрической конфигурации молекул:

А – многовалентный атом;

Х – атомы, связанные с атомом А;

n – число атомов Х;

Е – неподеленная пара электронов

m – количество неподеленных электронных пар.

Тогда формула молекулы по Гиллеспи записывается так: AX_nE_m .

Геометрия молекулы зависит от суммы n + m. Эта сумма определяет количество вершин той геометрической фигуры, которая соответствует пространственному строению молекулы. Так, молекулы типа АХ₂ (ВеН₂) всегда линейны, так как максимальное отталкивание двух электронных пар располагает их на концах диаметра условной сферы.

Три связывающие электронные пары молекул типа АХ₃ (ВF₃, AlF₃), максимально удаленные друг от друга, образуют правильный треугольник. В этом случае угол Х–А–Х равен 120⁰. Молекула с тремя электронными парами (n + m = 3) случае угол Х–А–Х равен 120ксимально удаленные друг от друга ар располагает их на концах диаметра условной сферыть, кот может соответствовать типу АХ₂Е (SnF₂). В этом случае угол Х–А–Х станет меньше 120⁰, треугольник станет неправильным, так как отталкивание между электронами несвязывающей неподеленной пары центрального атома (А) и связывающей пары сильнее, чем между электронами связывающих пар.

Четыре связывающие пары электронов в пространстве образуют тетраэдр. По Гиллеспи, это тип АХ₄ (СН₄). Угол Х–А–Х составляет 109⁰28^/. Молекула с четырьмя электронными парами (n + m = 4) может соответствовать типам АХ₃Е (NH₃) и АХ₂Е₂ (Н₂О). Разное по силе отталкивание связывающих и несвязывающих электронных пар приводит к искажению тетраэдрической структуры молекул. Так, в молекуле аммиака угол между связывающими парами (валентный угол ) составляет 107,3⁰, в молекуле воды – 104,5⁰.

Пять связывающих электронных пар в пространстве образуют тригональную бипирамиду и соответствуют типу АХ₅. (PF₅, PCl₅). Наличие несвязывающей неподеленной пары соответствует типу АХ₄Е (SF₄).

Шесть связывающих электронных пар образуют в пространстве октаэдр. Это соответствует типу АХ₆ (SF₆). Наличие несвязывающих электронных пар у центрального атома приводит к искажению октаэдра: тип АХ₅Е (IF₅) – квадратная пирамида, тип АХ₄Е₂ (XeF₄) – квадрат.

Следует отметить, что дипольный момент (µ) молекул типа AX_n, в которых все валентные электронные пары являются связывающими, т.е. отсутствуют несвязывающие электронные пары у центрального атома (m =0), равен нулю. Это обусловлено симметричным расположением векторов дипольных моментов связей А–Х, при котором суммарный вектор равен нулю. В молекулах типа AX_nE_m нарушение симметрии расположения электронных пар в случаях AX₂E, AX₃E, AX₂E₂, AX₄E, AX₃E₂, AX₅E приводит к отличному от нуля суммарному дипольному моменту. В молекулах типа AX₂E₃, AX₄E₂ сохраняется некоторая степень симметрии связей и неподеленных электронных пар и суммарный дипольный момент молекулы равен нулю (Рис.5.3.).

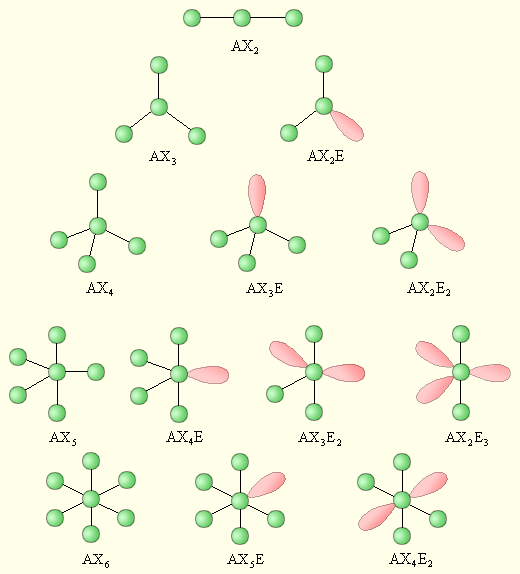
Рис. 5.3. Формулы молекул по Гиллеспи и соответствующие им пространственные структуры.

Отметим, что электроны, описываемые АО, в соответствии с принципом Паули должны иметь противоположно направленные спины, то есть в методе ВС все спины спарены, и все молекулы должны быть диамагнитны. Следовательно, методе ВС принципиально не может объяснить магнитные свойства молекул, в частности, парамагнитные свойства молекулы кислорода. Не объяснима устойчивость некоторых ионов, в частности катиона Н₂⁺, включающего систему из двух протонов и электрона. С позиций метода ВС отсутствие пары электронов означает отсутствие связи и должно привести к распаду катиона на протон и атом водорода. Экспериментально установлено, что энергия связи молекулы кислорода (О₂) и фтора (F₂) меньше, чем ионизированной молекулы кислорода (О₂⁺) и фтора (F₂⁺) . Так, энергия разрыва связи в молекуле F₂ составляет 155 кДж/моль, а в молекулярном ионе F₂⁺ – 320 кДж/моль; аналогичные величины для молекул О₂ и молекулярного иона О₂⁺ составляют соответственно 494 и 642 кДж/моль. Валентность азота в аммиаке равна трем, а в ионе аммония – четырем. Представления метода ВС в этом случае приводят к противоположным выводам. Связь должна стать менее прочной, так как удаление одного электрона разрушает одну из двух связывающих электронных пар.