Уравнение Бернулли для элементарной струйки идеальной жидкости

Рассмотрим элементарную струйку идеальной жидкости. Выделим в ней отсек 1-2, ограниченный сечениями 1-1 и 2-2. В сечении 1-1 площадью dS₁(рис.20), действует давление p₁, а скорость движения жидкости U₁. В сечении 2-2 – давление p₂, площадь dS₂ , скорость U₂. Центры тяжести выбранных сечений расположены на высотах Z₁ и Z₂ над плоскостью х₀у. Если бы жидкость, рас-

Рис. 20. Элементарная струйка положенная в трубке тока между сече-

идеальной жидкости ниями 1-1 и 2-2 былa неподвижна,

положенная в трубке тока между сече-

ниями 1-1 и 2-2 былa неподвижна,

то можно было бы записать уравнение равновесия жидкости в соответствии с основным уравнением гидростатики

.

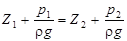или умножив все члены на g, получим

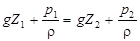. (74)

Уравнение (74) описывает закон сохранения потенциальной энергии в условиях покоя жидкости. Действительно, если 1 кг жидкости поднять на высоту Z₁ над условной плоскостью сравнения, а под действием давления в этом сечении жидкость в трубке пьезометра сможет подняться еще на высоту 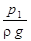, то она обладает суммарной удельной потенциальной энергией единицы массы

Е¹ _пот= 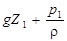, 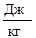. (75)

При движении жидкость обладает также кинетической энергией. Удельная кинетическая энергия единицы массы жидкости для первого сечения

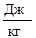, . (76)

Присоединяя значение кинетической энергии к суммарной потенциальной энергии жидкости, в состоянии покоя получим уравнение, характеризующее равновесие жидкости в условиях движения

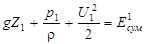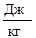, . (77)

А так как действует закон сохранения энергии, то можно записать

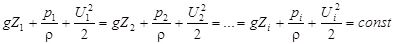. (78)

Уравнение (78) устанавливает связь между геометрическим положением, давлением и скоростью жидкости в произвольном сечении. Оно называется уравнением Бернулли для элементарной струйки идеальной жидкости.

Анализируя уравнение можно увидеть, что расширение струйки (увеличение площади живого сечения струйки) приводит к уменьшению скорости струйки, а это уменьшает кинетическую энергию. А так как полная энергия струйки в любом сечении является величиной постоянной, т.е. сумма членов является константой, то увеличивается потенциальная энергия давления жидкости в данном сечении. И наоборот, уменьшение площади живого сечения струйки вызывает увеличение скорости и, следовательно, увеличение кинетической энергии, что приводит к уменьшению энергии потенциальной и соответственному падению давления. Проведем анализ размерности всех членов входящих в уравнение (78) помня о том, что силы инерции и силы тяжести были отнесены к единице массы жидкости, то есть члены уравнения, в которых присутствует скорость либо ускорение необходимо помножить на .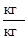

gZ = = = = .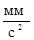

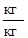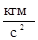
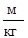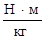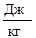Мы получили размерность удельной энергии, энергии отнесенной к единице массы жидкости ( 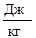- это энергия 1 кг жидкости).

= = = ,

= = = .

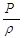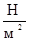
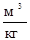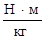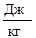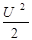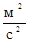
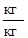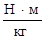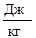Уравнение (78) иллюстрирует энергетический смысл уравнения Бернулли – в любом сечении струйка жидкости обладает одной и той же суммарной энергией. Энергия трансформируется переходя из одного вида в другой при изменении условий течения, но сумма потенциальной и кинетической энергии остается постоянной. Рассмотрим еще один вид уравнения Бернулли – вид иллюстрирующий геометрический смысл. Для этого разделим все члены уравнения (78) на g

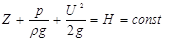. (79)

При геометрической интерпретации трактовки уравнения Бернулли все члены уравнения (79) могут быть представлены отрезками. Здесь

z – высота положения выбранного сечения над плоскостью сравнения, м;

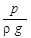- пьезометрическая высота или высота, на которую поднимется жидкость под действием давления в заданной точке, если в эту точку поместить пьезометр, м;

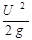- скоростной напор, м;

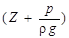- полный гидростатический напор, м;

Н – полный гидродинамический напор, м.

Все члены уравнения (79) имеют линейную размерность – м.

Трубка Пито

Высота скоростного напора не является чем-то сугубо теоретическим. Как и остальные члены уравнения Бернулли (79) она измеряется, и для ее определения используется специальное измерительное приспособление трубка Пито.

Рис. 21. Трубка Пито Трубка Пито состоит из двух трубок – одной прямой, которая является пьезометром, и другой - изогнутой под углом 90⁰ (рис. 21). Обе трубки скомпонованы в одном корпусе.

В прямой трубке жидкость поднимается на пьезометрическую высоту 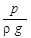, а изогнутая трубка, направленная навстречу потоку, воспринимает не только

статическое давление, но и динамическое. В ней жидкость поднимется на высоту ( 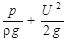). По разности показаний трубок ∆h = 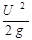, можно измерять скорость

U = 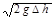, м/с. (80)

На практике каждая изготовленная трубка Пито имеет свой поправочный коэффициент, который учитывает как потери энергии, так и то, что концы трубок расположены в разных, а не в одной точке.