ЛЕКЦИЯ 3. Задачи базового уровня ЕГЭ.

Задача №8(Связь между давлением и средней кинетической энергией, абсолютная температура, связь температуры со средней кинетической энергией, уравнение Менделеева – Клапейрона, изопроцессы).

1) Задача. Четыре бруска одинаковой массы изготовлены из алюминия (молярная масса 27 г/моль), золота (молярная масса 197 г/моль), свинца (молярная масса 207 г/моль) и цинка (молярная масса 65 г/моль). Наибольшее число атомов содержится в бруске из

1) алюминия, 2) золота, 3) свинца, 4) цинка.

Решение: Молярная масса указывает на массу атома. Чем меньше молярная масса, тем легче атом. Значит, тем большее количество атомов будет содержаться.

Ответ: 1; алюминий.

2) Задача. Двое учеников прочитали в учебнике про эксперименты Ж. Перрена по наблюдению броуновского движения частиц в жидкости. На следующий день, отвечая на уроке, первый ученик сказал, что интенсивность броуновского движения зависит от времени, а второй ученик сказал, что интенсивность броуновского движения возрастает с увеличением температуры жидкости. После этого учитель заключил, что

1) правильно ответил только первый ученик ,

2) правильно ответил только второй ученик ,

3) правильно ответили оба ученика ,

4) оба ученика ответили неправильно .

Ответ: 2.

3) Задача. Какое из описанных ниже движений частицы можно считать броуновским?

1) движение пылинки вместе с потоком воздуха,

2) движение частиц сажи в вертикально поднимающемся столбе дыма,

3) движение мелких спор ликоподия в капле воды,

4) все три описанных движения.

Ответ: 3.

4) Задача. По какой причине наблюдается броуновское движение мелких пылинок в жидкости?

1) Молекулы жидкости при хаотическом тепловом движении сталкиваются с пылинками и беспорядочно толкают их, сообщая им импульс;

2) В жидкости существуют упорядоченные потоки, которые и заставляют пылинки двигаться;

3) Пылинки изначально обладают собственным импульсом, который и наблюдается в опытах;

4) Броуновское движение обусловлено всеми перечисленными причинами.

Ответ: 1.

5) Задача. В двух закрытых сосудах находятся по одному молю идеальных газов: в первом сосуде - водород, во втором сосуде - гелий. Среднеквадратичная скорость теплового движения молекул водорода 1500 м/с, атомов гелия - 750 м/с. Абсолютная температура гелия

1) в 2 раза больше, чем температура водорода ;

2) в 2 раза меньше, чем температура водорода ;

3) в 4 раза больше, чем температура водорода ;

4) равна температуре водорода .

Решение. Внутренняя энергия газа – сумма кинетических энергий движений молекул. Среднеквадратичная скорость теплового движения молекул водорода в два раза больше чем атомов гелия. Следовательно, и кинетическая энергия движения молекул водорода в два раза больше кинетической энергии движения атомов гелия. Соответственно, и внутренняя энергия, также и температура у водорода будут в два раза выше, чем у гелия.

Ответ: 2.

6) Задача. Дима и Лена схематически изобразили на доске сосуд, в котором находится идеальный газ.

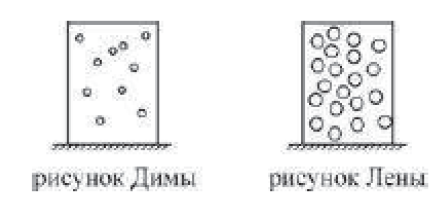
Отвечающим модели идеального газа можно признать рисунок, сделанный

А) Димой, Б) Леной

1) только А, 2) только Б, 3) и А, и Б, 4) ни А, ни Б .

Ответ: 1.

Задача №9.(Работа в термодинамике, первый закон термодинамики, КПД тепловой машины).

1) 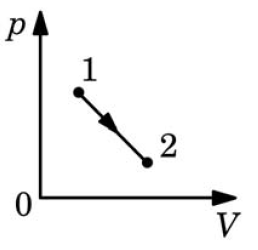Задача. В процессе, изображенном на pV–диаграмме, температура некоторой массы идеального газа

1) все время убывает , 2) все время возрастает , 3) все время остается неизменной , 4) может как убывать, так и возрастать .

Решение: 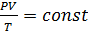. При уменьшении давления и увеличении объема газа температура может как падать так и расти.

Ответ: 4.

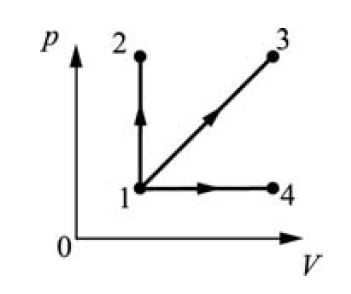2) Задача. В каком из изображенных на pV–диаграмме процессов температура идеального газа возрастает?

1) 1à2 , 2) 1à3 , 3) 1à4 ,

4) во всех трех процессах .

Решение: 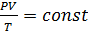. В первом процессе температура падает. Во втором процессе температура падает. В третьем процессе температура возрастает пропорционально увеличению давлению.

Ответ: 3.

3) Задача. Два различных идеальных газа в количестве 1 моль каждый находятся в двух разных закрытых сосудах. В таблице приведены

давления этих газов и занимаемые ими объемы.

Из таблицы следует, что

1) температура газа 1 больше температуры газа 2 ,

2) температура газа 1 меньше температуры газа 2 ,

3) температуры газа 1 и газа 2 одинаковы ,

4) нельзя сделать вывод о соотношении температур газа 1 и газа 2 .

Ответ: 2.

4) Задача. Закрытый цилиндрический сосуд разделён на две части подвижным поршнем массой 1 кг, который может двигаться без трения. В первой части находится 5 молей идеального газа, во второй 15 молей этого же газа. Температуры газов в обеих частях сосуда одинаковы. Поршень находится в равновесии. На каком из приведённых рисунков правильно показано расположение этого сосуда с газом?

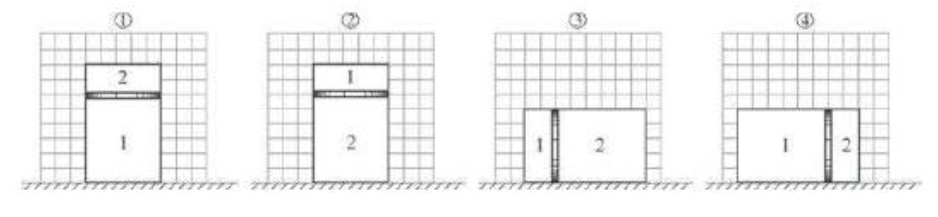
1) 1 2) 2 3) 3 4) 4

Решение: В горизонтальном расположении газ в сосуде будет иметь состояние динамического равновесия: 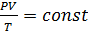. Здесь 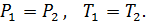Значит, объем газа в первой части будет в три раза меньше объема газа во второй части сосуда.

Ответ: 3.

5) Задача. На графиках представлены зависимости концентрации n и температуры Т идеального газа от времени t.

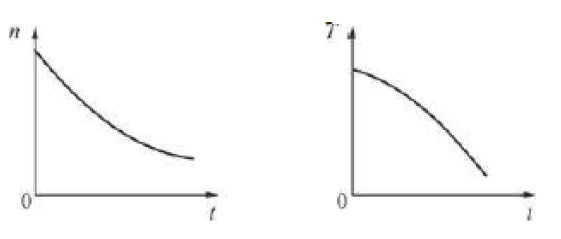
Из этих зависимостей следует, что давление газа с течением времени

1) увеличивалось 2) уменьшалось 3) не изменялось 4) сначала увеличивалось, а потом уменьшалось.

Ответ: 2.

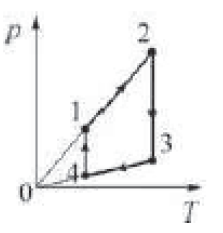
6) Задача. На рисунке изображён циклический процесс для идеального ргаза. Изохорическому нагреванию газа соответствует участок

1) 1-2 2) 2-3 3) 3-4 4) 4-1

Ответ: 1.

7) Задача. Первому телу сообщили количество теплоты 1 кДж, а второму - 2 кДж. Массы тел одинаковы. В результате температура первого тела повысилась на 100 К, а второго - повысилась на 50 К. Можно утверждать, что удельная теплоёмкость у вещества первого тела

1) больше, чем у вещества второго тела ,

2) меньше, чем у вещества второго тела ,

3) такая же, как у вещества второго тела ,

4) не может быть соотнесена с удельной теплоёмкостью вещества второго тела .

Решение: 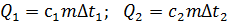. Подставим известные значения и видим, что верным является второе утверждение.

Ответ: 2.

Задача №10.(Относительная влажность воздуха, количество теплоты).

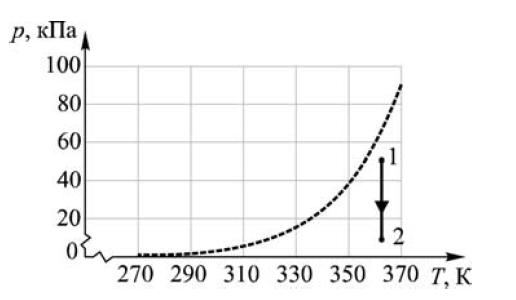1) Задача. На рисунке изображены: пунктирной линией – график зависимости давления p насыщенных паров воды от температуры T, и сплошной линией – процесс 1–2 изменения парциального давления паров воды. По мере такого изменения парциального давления паров воды абсолютная влажность воздуха:

1) увеличивается.

2) уменьшается.

3) не изменяется.

4) может как увеличиваться, так и уменьшаться.

Решение: 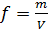. Эта формула определения абсолютной влажности воздуха, где m– масса водяного пара в объеме V влажного воздуха. При неизменной температуры давление в процессе 1-2 падает. Соответственно объем V увеличивается. Значит и парциального давления паров воды уменьшится.

Ответ: 2.

2) Задача. Два бруска, сделанные из разных металлов, приводят в тепловой контакт. После установления теплового равновесия у этих брусков будут одинаковыми

1) внутренние энергии,

2) среднеквадратичные скорости молекул,

3) температуры,

4) все три вышеуказанные характеристики.

Решение: Тепловое равновесие установится тогда, когда температуры тел будут одинаковыми, то есть, когда прекратится теплопередача. Внутренняя энергия тела и среднеквадратичная скорость молекул имеют прямо пропорциональную связь. И нет прямой связи с температурой тела.

Ответ: 3.

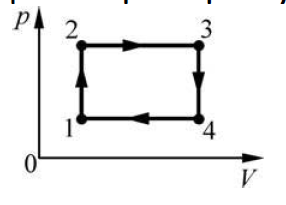3) Задача. На pV–диаграмме изображен циклический процесс 1 2 3 4 1, совершаемый над идеальным газом. На участке 1–2 газ обменивается с окружающими телами количеством теплоты 1245 Дж, а на участке 2–3 – количеством теплоты 2075 Дж. Чему равен КПД этого циклического процесса, если газ за один цикл совершает работу 207,5 Дж?

1) 16,7% 2) 10% 3) 6,25% 4) 25%

Решение:

Ответ: 3.

4) Задача. Порции идеального газа сообщили некоторое количество теплоты. При этом газ совершил положительную работу. В результате внутренняя энергия порции газа

1) увеличилась

2) уменьшилась

3) не изменилась

4) могла и увеличится, и уменьшиться, и остаться неизменной

Ответ: 4.

5) Задача. КПД идеальной тепловой машины зависит

1) от температуры холодильника, температуры нагревателя и рода рабочего тела

2) только от рода рабочего тела

3) только от температуры холодильника

4) только от температуры холодильника и температуры нагревателя

Ответ: 4.