Меркаторская картографическая проекция, её свойства. Локсодромия и её свойства. Вычисления локсодромического курса и расстояния по географическим координатам.

Меркаторская проекция относится к классу цилиндрических нормальных равноугольных проекций, в которых параллели нормальной сетки есть параллельные прямые, а расстояние между меридианами пропорциональны соответствующим разностям долгот.

Для получения меркаторской проекции необходимо спроектировать меридианы и параллели Земного шара на внутреннюю поверхность цилиндра касательного к земле в районе экватора. При разворачивании цилиндра в плоскость параллели растянутся и станут по длине равными экватору и параллельными ему. Таким образом получается прямоугольная сетка параллелей и меридианов, расположенных на равных расстояниях друг относительно друга. На такой сетке локсодромия, пересекающая все меридианы под одним углом, изобразится прямой линией.

Однако полученная проекция не является равноугольной, так как параллели на ней растянулись пропорционально секансу широты, а величина меридианов осталась неизменной. Для того, чтобы проекция стала равноугольной необходимо произвести растяжение меридианов в каждой точке, так же как растянуты параллели, т. е. пропорционально секансу широты точки.

Ортодромия, пересекающая параллельные меридианы под разными углами, на меркаторской проекции изображается кривой линией, что усложняет прокладку дуги большого круга, что затрудняет плавание по кратчайшему расстоянию.

Меркаторская проекция имеет и другие недостатки:

- проекция не сохраняет равенство площадей;

- невозможно создание меркаторской карты для приполюсных районов;

- масштаб на картах меркаторской проекции изменяется с широтой, что вносит искажения измеренных циркулем расстояния даже в пределах одного листа карты.

Кривую на поверхности Земли, пересекающую все мередианы под одним и тем же углом, называют локсодромией, что с греческого переводится. как «косой бег».

Расстояние между двумя точками на сфере по локсодромии не является кратчайшим и её применение в мореплавании обьясняется исключительным удобством использования компасов.

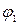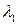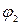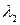Уравнение локсодромии между точками с координатами , и , для эллипсоида имеет вид:

,

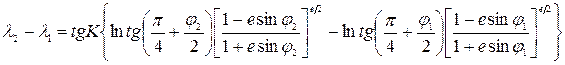где 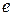-эксцентриситет эллипсоида. Уравнение локсодромии на шаре выглядит так:

.

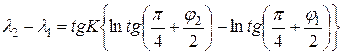Из данного уравнения можно получить аналитическое выражение для локсодромичес-кого курса К :

.

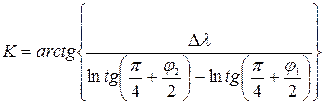Расстояние Sмежду двумя точками выражается следующим образом. В общем случае

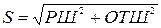, где РШ= 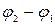, ОТШ= .

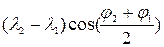5. Ортодромия, ортодромическая поправка. Способы построения ортодромии на картах меркаторской проекции.

Ортодромия (из др.-греч. ὀρθός «прямой» + δρόμος «бег, путь») — кратчайшая линия между двумя точками на поверхности Земли. В отличие от локсодромии ортодромия пересекает меридианы под разными углами. В судо- и самолётовождении, где Земля принимается за шар, ортодромия представляет собой дугу большого круга.

Экватор и меридианы являются частными случаями ортодромии. Через две точки на земной поверхности, расположенные не на противоположных концах одного диаметра Земли, можно провести только одну ортодромию.

В большинстве картографических проекций ортодромии изображаются кривыми линиями (за исключением, быть может, меридианов и экватора). Это неудобно для прокладки кратчайших маршрутов. В гномонической проекции все ортодромии изображены прямыми линиями.

Параллели (за исключением экватора) не являются ортодромиями.

Ортодромической поправкойназывается угол y между локсодромией и касательной к ортодромии.

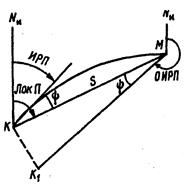
Ортодромическая поправка является поправкой за кривизну изображения дуги большого круга на меркаторской карте. Она определяется с помощью формулы:

,

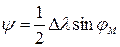где 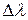- разность долгод; 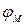- средняя широта.

При плавании по дуге большого круга ее траекторию заменяют хордами – отрезками локсодромии. Причем долготный интервал ходы равен 4-6 градусов.

На практике используют следующие способы расчета направлений участков локсодромии для плавания по дуге большого круга:

- с помощью ортодромических поправок;

- с помощью карт гномонической проекции;

- с помощью специальной номограммы;

- с применением средств вычислительной техники.

Использование ортодромической поправки. Необходимо выполнить следующие действия:

1. Определить долготный интервал изменения курсов 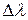и провести соответствующие ему меридианы от пункта отхода к пункту прихода.

2. По координатам начальной и конечной точек плавания на карте меркаторской проекции проложить отрезок локсодромии между этими точками и измерить исходный курс (рис.).

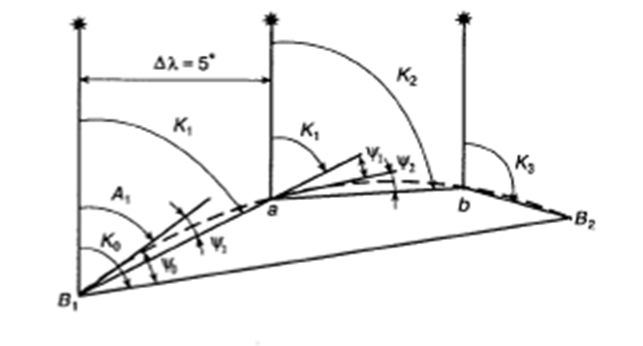
3. Начальную ортодромическую поправку 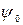выбрать из таблицы 2.12 МТ-2000 или рассчитать по формуле 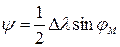. Учесть, что в северном полушарии при движении на восток знак 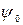положителен, а при движении на запад – отрицателен. В южном полушарии – наоборот.

4. Рассчитать направление ортодромии в пункте отхода:

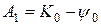
5. Рассчитать курс первой хорды: ,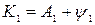

где 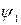- ортодромическая поправка первого курса, выбираемая по широте первой точки 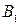и принятому долготному интервалу .

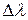6. От исходной точки 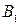по направлению 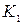до пересечения с меридианом 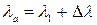провести первую хорду дуги большого круга. В полученной точке а рассчитать направление второй хорды ,

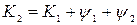где 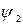- ортодромическая поправка второго курса, выбираемая по широте точки а и принятому долготному интервалу .

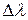7 . Провести вторую хорду от точки а до меридиана .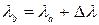

Аналогично рассчитать и проложить все последующие хорды. Когда до пункта прихода остается приращение долготы меньше принятого интервала, хорда не рассчитывается, заключительный отрезок локсодромии прокладывается от точки на последнем промежуточном меридиане непосредственно в пункт прихода.

Использование специальной номограммы.По ней определяется начальное направление дуги большого круга 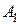, затем – как в первом способе через ортодромические поправки.

Использование вычислительной техники.Для выбранного приращения долгот локсодромические курсы рассчитываются по формулам:

Начальный курс рассчитаем по формуле:

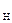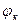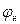K' = arctg(sin[РД]/(tg *cos -sin 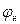*cos РД)),

где РД – разность долгот между начальной и конечной точек; 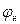, 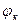- широта начальной и конечной точек.

Для значения долгот 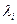через 10 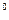находим значения широт 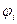по формуле:

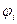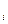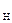=arctg((sin РД /tg K +sin 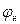*cos РД 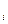)/cos ).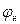

6. Классификация карт, используемых в судовождении. Содержание карт. Руководства и пособия для плавания. Требования конвенции СОЛАС в отношении карт и пособий для плавания.

Морской картой называется построенное по определенному закону, уменьшенное и обобщенное изображение на плоскости поверхности океанов и морей Земли, передающее размещение и взаимосвязь различных объектов и явлений природы при помощи условных знаков.

Морские карты издаются главным образом в меркаторской проекции и по своему назначению подразделяются на:

1. Навигационные предназначаются для ведения счисления пути и определения места судна в море.

2. Вспомогательные и справочные морские карты, под названием которых объединены различные картографические издания.

Общенавигационные карты являются основной подгруппой морских карт, обеспечивающих безопасность мореплавания.

В зависимости от масштаба общенавигационные марские карты подразделяются на: генеральные, имеющие масштаб от 1:1000000 до 1:5000000; путевые – от 1:100000; частные – от 1:25000 до 1:100000; планы – от 1:100 (при производстве различных гидрографических работ) до 1:25000.

Частные карты содержат все навигационные подробности.

Содержанием карты называется совокупность всех наносимых на карту элементов. Оно включает в себя :

- математическую основу карты;

- общегеографическую нагрузку;

- специальную нагрузку;

- элементы оформления.