Синтез решетчатого фильтра

Несмотря на близость РФ и АР фильтров, использование РФ требует введения новых понятий и соот­ношений, на основе которых выводится структура РФ. Прежде всего, необходимо остановиться на выводе ре­куррентных соотношений, которые носят название алгоритма Левинсона-Дарбина. Алгоритм позволяет вы­числять для р-го порядка коэффициенты АР и отражения РФ по найденным коэффициентам АР модели сигнала 1…р порядков.

По аналогии с фильтром прямого предсказания для сигнала, описываемого моделью АР р-го порядка, можно ввести фильтр обратного предсказания, описываемый выражением

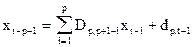, (26)

где 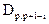- коэффициенты фильтра обратного предсказания, состоящего из р звеньев, 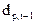- ошибка обратного предсказания на выходе р-го звена фильтра. Уравнение описывает регрессию значения случайного процесса 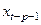на последующие 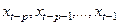. Значения коэффициентов фильтра обратного предсказания находятся с помощью системы урав­нений, аналогичной системе уравнений Юла-Уокера. Объединяя уравнения (2.4а) и (2.4б), можно представить обобщенные уравнения Юла-Уокера в матричном виде

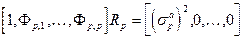, (27)

где 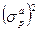-квадрат СКО, равный дисперсии ошибки прямого предсказания, R_p - корреляционная матрица (p+1) –го порядка

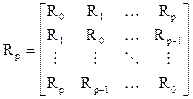. (28)

Чтобы не выходить за рамки общепринятых в теории решетчатых фильтров обозначений (например [4]), в дальнейшем изложении будет использоваться замена 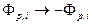и .

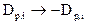Умножив левую и правую части уравнения на , 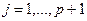и усреднив, легко получить уравнение Юла-Уо­кера для фильтра обратного предсказания, аналогичное (27)

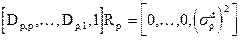, (29)

где 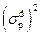- дисперсия ошибки обратного предсказания на выходе p-го звена фильтра обратного предсказа­ния. Объединив матричные уравнения (27) и (29) можно записать общее уравнение

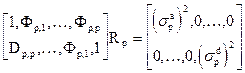. (30)

Очевидно, что для (р+1)-звенного фильтра должно так же выполняться соотношение типа

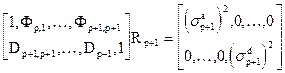. (31)

Но, как показано в [4], от матричного уравнения (30) можно перейти к матричному уравнению (31) лишь в том случае, если коэффициенты фильтров прямого и обратного предсказания p-го порядка связаны с коэффи­циентами фильтра (p+1)-го порядка следующим образом

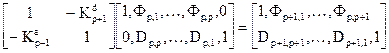, (32)

где 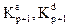- некоторые, так называемые, коэффициенты отражения. Умножив справа левую и правую части матричного уравнения (32), на корреляционную матрицу 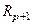можно показать, что коэффициенты отражения удовлетворяют соотношениям

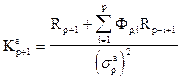, (33а)

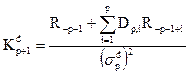. (33б)

Величины, входящие в соотношения (33а) и (33б), описываемые выражениями

, (34а)

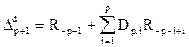, (34б)

как будет показано ниже, интерпретируются как взаимная корреляция ошибок прямого и обратного предска­зания при единичной задержке. Для скалярного случая справедливы равенства

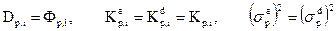. (35)

Используя соотношения (23а), (23б) и учитывая (23), алгоритм Левинсона-Дарбина, позволяющий вычислять коэффициенты АР по коэффициентам отражения, можно предста­вить в виде

(36)

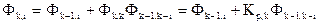, (37)

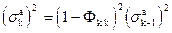, (38)

с инициацией

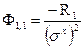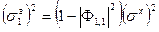, . (39)

Найденный алгоритм Левинсона-Дарбина позволяет получить структуру РФ. Формулы (1) и (37) дают выражение

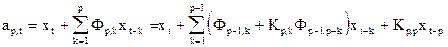, (40)

которое с помощью (26) и учетом (35) для р-го звена приводится к виду

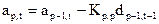. (41)

Аналогично можно найти выражение для ошибки обратного предсказания в р звене

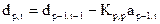. (42)

Полученные выражения (41) и (42) дают возможность представить структуру РФ в виде, изображенном на рисунке 3.

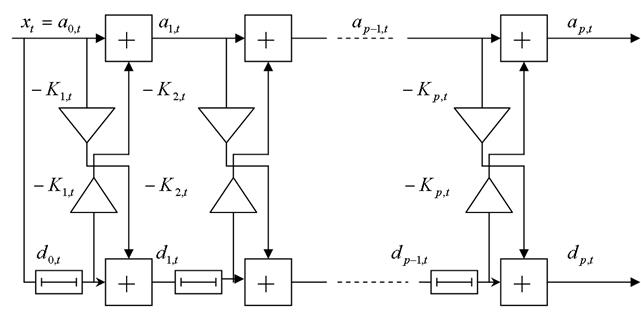
Рисунок 3. Обеляющий РФ.

При поступлении сигнала на вход фильтра на выходе каждого звена фильтра появятся ошибки пред­сказания вперед и назад. Как видно из рисунка 3 ошибки предсказания вперед и назад связаны друг с другом соот­ношениями (41) и (42).

Можно показать, используя соотношение (42), что решение задачи минимизации дисперсии ошибки предсказания 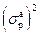относительно коэффициента отражения К_p дает следующее выражение для коэффици­ента отражения

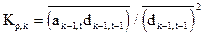. (43)

К этому же соотношению можно придти путем несложных преобразований выражений (41) и (42). Таким обра­зом, РФ, коэффициенты отражения которого определяются алгоритмом Левинсона-Дарбина, минимизирует дисперсию ошибки предсказания. Выражение (43) дает удобную оценку коэффициентов отражения РФ, позволяющее обновлять их при адаптации фильтра.

Из рисунка 3 видно, что текущий отсчет случайного процесса можно представить в виде

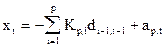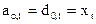, , (44)

т.е. взвешенным суммированием ошибок обратного предсказания в предшествующий момент времени с ко­эффициентами веса, равными коэффициентам отражения. Случайная величина х_t, представленная в виде (44), полностью определяется коэффициентами веса, роль которых играют коэффициенты отра­жения. Таким образом, коэффициенты отражения полностью характеризуют случайный процесс в рамках мо­дели АР. Это свойство коэффициентов отражения РФ позволяет использовать их в качестве информативного признака при распознавании и спектральном оценивании.