Метод прямого интегрирования

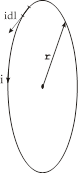Основная задача: зная токи, требуется найти магнитное поле во всем пространстве (вектора 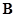и ).

Пример: магнитное поле в центре кольца. Кольцо разбивается на множество элементов 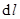. Используется принцип суперпозиции.

,

Закон полного тока

Циркуляцией вектора по заданному замкнутому контуру называется интеграл

,

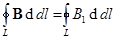где 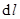- вектор элементарной длины контура, направленной вдоль обхода контура, - составляющая вектора 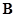в направлении касательной к контуру, - угол между векторами 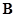и .

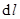Закон полного тока: циркуляция вектора 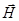по замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром:

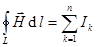
Данный закон справедлив для постоянного магнитного поля.

Некоторые формулы

1. Поле тороида.

Тороид – кольцевая катушка, витки которой намотаны на сердечник, имеющий форму тора. Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.

Линии магнитной индукции в данном случае есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса 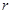. Тогда, по теореме о циркуляции , откуда следует, что магнитная индукция тороида (в вакууме): , где - число витков тороида.

2. Поле соленоида.

Для нахождения магнитной индукции выберем замкнутый прямоугольный контур ABCDA как показано на рисунке. Циркуляция вектора 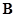по замкнутому контуру равна:

,

интеграл можно представить в виде четырех интегралов по AB, BC, CD, DA. На участках AB и CD контур перпендикулярен линиям магнитной индукции и . На участке вне соленоида . На участке DA циркуляция вектор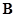а равна , следовательно

, откуда

.

Получили, что поле внутри соленоида однородно (краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают).