Связь потенциала(j) и напряженности(E)
Различают два вида полей: потенциальные и вихревые поля. Если работа по замкнутому пути равна нулю, то поле потенциальное. Форма пути не играет роли. Пример: гравитационное и электростатическое поля (подтверждено опытами). Если же такая работа не равна нулю, то поле называется вихревым. Пример: магнитное поле. Найдем взаимосвязь между напряженностью электростатического поля, являющейся его силовой характеристикой, и потенциалом – энергетической характеристики поля.
В потенциальных полях работа равна:
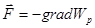 ;
;
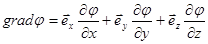 .
.
Градиент скалярной величины – это вектор.
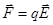 ;
;
 ;
;
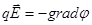 ,
,
откуда:
j= 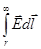 ,
,  или
или 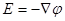 .
.
Т.е. напряженность 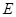 поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности
поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности 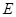 поля направлен в сторону убывания потенциала.
поля направлен в сторону убывания потенциала.
Для графического представления распределения потенциала электростатического поля, как и в случае поля тяготения, пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал имеет одно и тоже значение.
Если поле создается точечным зарядом, то его потенциал равен:  . Таким образом эквипотенциальные поверхности в данном случае – концентрические сферы. Линии напряженности всегда нормальны эквипотенциальным поверхностям, т.к. работа по перемещению заряженного тела по эквипотенциальной поверхности равна нулю.
. Таким образом эквипотенциальные поверхности в данном случае – концентрические сферы. Линии напряженности всегда нормальны эквипотенциальным поверхностям, т.к. работа по перемещению заряженного тела по эквипотенциальной поверхности равна нулю.
Емкость
Металлическому телу сообщают заряд 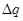 .
.
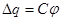
 .
.
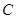 – коэффициент, связывающий изменение заряда уединенного тела с изменением его потенциала называют емкостью. Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
– коэффициент, связывающий изменение заряда уединенного тела с изменением его потенциала называют емкостью. Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Если есть 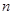 тел, рассматриваются коэффициенты
тел, рассматриваются коэффициенты 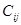 (но это в электротехнике).
(но это в электротехнике).
Ниже приведены формулы для вычисления емкостей некоторых конденсаторов. Вывод для цилиндрического и шарового конденсаторов предлагаем вам сделать самостоятельно.
Плоский конденсатор:
Так как поле сосредоточено внутри конденсатора, то линии напряженности будут начинаться на одной обкладке и кончаются на другой, поэтому свободные заряды, возникающие на разных обкладках, являются равными по модулю разноименными зарядами.
 ;
;
Пусть конденсатор состоит из двух параллельных металлических пластин площадью 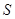 каждая, расположенных на расстоянии
каждая, расположенных на расстоянии  друг от друга и имеющих заряды
друг от друга и имеющих заряды 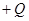 и
и  . Если расстояние между пластинами мало по сравнению с размерами пластин, то краевыми эффектами можно пренебречь и поле между обкладками можно считать однородным. Его можно рассчитать, используя формулы для потенциала и напряженности. При наличии диэлектрика между обкладками разность потенциала между ними равна:
. Если расстояние между пластинами мало по сравнению с размерами пластин, то краевыми эффектами можно пренебречь и поле между обкладками можно считать однородным. Его можно рассчитать, используя формулы для потенциала и напряженности. При наличии диэлектрика между обкладками разность потенциала между ними равна:
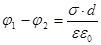 ,
,
тогда заменяя  , получаем выражение для емкости конденсатора:
, получаем выражение для емкости конденсатора:
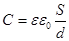
Цилиндрический конденсатор:
 .
.
Шаровой конденсатор:
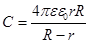 .
.
Дата добавления: 2021-03-18; просмотров: 445;











