Особенности несимметричных КЗ

При 3-ех фазном КЗ несимметрия отсутствует и напряжение в точке КЗ равно 0. При несимметричном КЗ в точке замыкания появляется напряжение обратной и нулевой последовательности, которые при нормальных условиях работы электрической сети отсутствуют. Под действием этих напряжений в сети будут протекать соответствующие токи, т.е в цепи с напряжением обратной и нулевой последовательностей, будут протекать токи обратной и нулевой последовательностей .

Элементы схемы в общем случае будут представлять для токов обратной, прямой, нулевой последовательностей не одинаковые сопротивления. При протекании токов различных последовательностей, будут создаваться падения напряжений различных последовательностей:

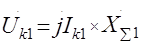(41.1)

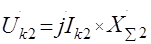(41.2)

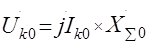(41.3)

В электрических системах существует ЭДС только прямой последовательности, а токи обратной и нулевой последовательностей определяются напряжениями в аварийных точках, т.е. напряжениями симметричных составляющих 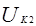и .

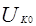Для симметрических составляющих напряжений в месте КЗ для каждой последовательности можно написать, что:

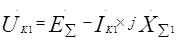(41.4)

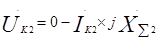(41.5)

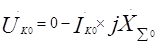, (41.6) где

U_k1, U_k2, U_k0, I_k1, I_k2, I_k0– симметричные составляющие напряжения и тока в месте короткого замыкания;

Е_Σ – результирующая ЭДС относительно точки КЗ;

X_Σ1, X_Σ2, X_Σ0– результирующие индуктивные сопротивления схем соответствующих последовательностей относительно точки КЗ.

Уравнения (41.1)-(41.3) или (41.4)-(41.6) содержат шесть неизвестных величин: три составляющие напряжения и три составляющие тока. Недостающие для определения этих величин уравнения легко получить из граничных условий, которыми характеризуется тот или иной вид несимметричного повреждения.

Задача нахождения токов и напряжений при рассматриваемом несимметричном переходном процессе по существу сводится к вычислению симметричных составляющих этих величин. Как только последние найдены, дальнейшее определение фазных величин токов и напряжений производится по известным соотношениям из теории симметричных составляющих.

42.Образование высших гармоник.

Пусть по одной или двум фазам статора протекает ток синхронной частоты f . Образующийся при этом пульсирующий магнитный поток остается в пространстве в одном и том же положении. Чтобы представить влияние этого потока на ротор, разложим его на 2 потока, вращающихся с синхронной угловой скоростью ω во взаимно противоположных направлениях (Рис.49)

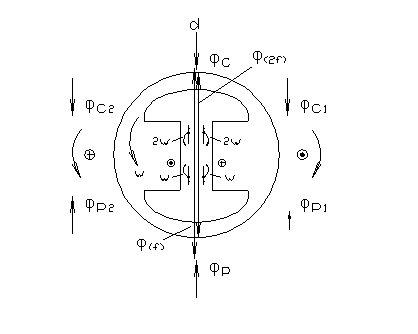
Рис.49

Поток, вращающийся в том же направлении, что и ротор, по отношению к последнему, неподвижен и соответственно взаимодействует с магнитным потоком обмотки возбуждения.

Другой поток, который вращается в противоположную сторону, по отношению к ротору будет иметь двойную скорость 2 ω. Поэтому в обмотке возбуждения будет наводиться ЭДС двойной синхронной частоты 2f. Обусловленный этой ЭДС, ток частоты 2f создает пульсирующий магнитный поток ротора с частотой 2f. Разложив эти потоки на Фр1 и Фр2, можно показать, что один из них вращается по отношению к статору с угловой скоростью (2 ω- ω) в сторону противоположную вращению ротора. Он оказывается неподвижным относительно потока вызвавшего пульсирующий с частотой 2f поток ротора и стремится его компенсировать.Другая составляющая потока Фр2 вращается со скоростью (2 ω+ ω= 3ω) в сторону вращения ротора. Этот магнитный поток наводит в статоре ЭДС тройной синхронной частоты 3f.В результате возникает ток той же частоты, который создает пульсирующее с 3f частотой магнитное поле статора.

Продолжая рассуждения, можно видеть, что каждая нечетная гармоника однофазного переменного тока статора вызывает очередную четную гармонику в обмотке возбуждения. И в свою очередь каждая четная гармоника тока в обмотке возбуждения вызывает следующую по порядку нечетную гармонику тока статора.