Терморезистивные характеристики
Рассмотрим температурные зависимости электросопротивления ВТСП материалов для различных составов – терморезистивные характеристики (ТРХ). Рассмотрение начнем с диэлектрических областей фазовых диаграмм – левее границы графиков (рис. 2.15). Это состояние реализуется либо при уменьшении содержания кислорода в Y-123, либо гетеровалентным замещением La3+ на Sr2+ в La2Cu2O4, либо замещением Ca2+ на Y3+ в Bi-2212 и т.д. Необходимо отметить, что изовалентное замещение как на магнитные, так и на немагнитные ионы дает совершенно разные результаты в зависимости от того, где находится замещаемый ион : в медь – кислородном слое или вне его. В первом случае ТС падает независимо от магнитных свойств атомов. Во втором случае влияние ионов на сверхпроводимость гораздо слабее.
Как видно из фазовых диаграмм (рис. 2.15), влияние состава на свойства оксидных соединений аналогично для разных материалов. Этот факт еще раз свидетельствует о том, что материалы имеют сходную структуру и механизмы их электропроводимости похожи. Рассмотрим, как изменяются электрофизические характеристики оксидных материалов при изменении их состава. Известно, что характеристика температурной зависимости сопротивления материала (ТРХ) может указать на механизмы электропроводности. Так, ТРХ YBa2Cu3Ox для различных х имеют существенные отличия (рис. 2.17).
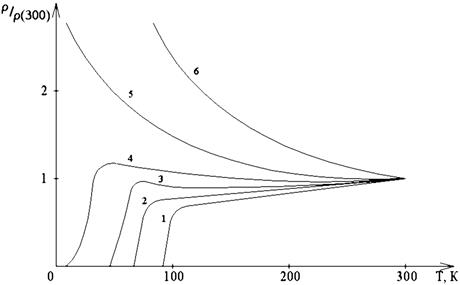
Рис. 2.17. Зависимость относительного электросопротивления YBa2Cu3Ox от температуры при различных содержаниях кислорода:
1 – x=6,53; 2 – x=6,5; 3 – x=6,44; 4 – x=6,32; 5 – x=6,25; 6 – x=6,17
Анализ графиков позволяет говорить о различных механизмах электропроводности. Образцы с минимумом кислорода (x<6,2) показывают экспоненциальный рост сопротивления с уменьшением температуры (рис. 2.17, 6).
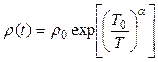 , (2.8)
, (2.8)
где α = 0,4…0,5;
Т0 – параметр модели.
Аналогичная зависимость наблюдалась и в системах La2-x SrxCuO6. Величина показателя α близка к теоретическому значению, полученному Шкловским и Эфросом для прыжковой проводимости в условиях, когда из-за кулоновских корреляций на уровне Ферми образуется мягкая квадратичная щель (q = 2) в плотности состояний:
g(t)~|E-EФ|q. (2.9)
Параметр Т0 (2.8) позволяет оценить радиус локализованного состояния аН:
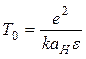 , (2.10)
, (2.10)
где е – заряд электрона;
ε – диэлектрическая проницаемость.
Оценка радиуса локализации дает величину 20 – 30 Аº. По мере приближения к точке перехода металл – изолятор, температурные зависимости ρ(T) трансформируются следующим образом. Вначале вместо закона Шкловского – Эфроса (α = ½) реализуется зависимость Мотта (α = ¼) для пиковой проводимости. В этом случае параметр Т0 выражается, как
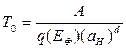 , (2.11)
, (2.11)
где А=16;
d=3;
q(Еф) – плотность состояний на уровне Ферми.
Еще ближе к точке перехода температурные кривые описываются степенным законом:
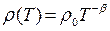 , (2.12)
, (2.12)
где β – параметр, зависящий от расстояния между дном зоны проводимости и уровнем Ферми.
При переходе к металлической фазе ТРХ приобретают линейный характер в нормальной области (рис. 2.17, 1, 2) и появляется переход в сверхпроводящее состояние. С увеличением содержания кислорода х температура перехода увеличивается.
Итак, анализ ТРХ позволяет составить следующую картину изменения ρ(T) при варьировании состава ВТСП. При минимальном содержании кислорода, концентрация носителей заряда весьма мала, их кулоновский потенциал экранируется слабо, поэтому для ρ(T) выполняется закон Шкловского–Эфроса, отвечающий прыжковой проводимости в условиях образования мягкой щели из-за дальнодействующих кулоновских корреляций типа отталкивания.
Когда число носителей заряда возрастает, кулоновский потенциал начинает экранироваться и транспортные свойства отвечают режиму моттовской прыжковой проводимости с переменной длиной прыжка. Несмотря на слоистое строение ВТСП, чаще всего наблюдается трехмерный закон Мотта (α = ¼), поскольку из-за увеличения длины прыжка (Т→0) начинаются межслоевые перескоки, приводящие к изотропизации процессов прыжковой проводимости. Наиболее широкий температурный интервал, где выполняется эта зависимость, характерен для Bi-2212 с большим расстоянием между слоями Cu-О. В области высоких температур происходит переход от режима прыжковой проводимости с переменной длиной прыжка (R~T-1/4) к режиму прыжковой проводимости на соседние центры с постоянной энергией активации (Еа).
Вблизи перехода металл – изолятор наблюдаются степенные зависимости ρ(T) (2.12).
На металлической стороне перехода с ростом концентрации кислорода становится возможен переход в сверхпроводящее состояние, вначале при низких, а затем при более высоких температурах. Нормальное состояние ВТСП характеризуется линейной, «металлической» зависимостью ρ(T).
Критический ток
Наиболее важным свойством сверхпроводников с точки зрения их практического применения является плотность транспортного критического тока jс. Большое значение имеет также изменение jс во внешнем магнитном поле.
Исследования ВТСП показали, что достижение в них высоких плотностей критического тока, в особенности в приложенном магнитном поле, является непростой научной и технологической задачей.
Установлено, что токонесущая способность образцов ВТСП зависит от их микроструктуры и, следовательно, от метода получения, как уже отмечалось (п. 1.2). Это обстоятельство является характерным и для низкотемпературных сверхпроводников, поскольку jс(H) определяется главным образом силой взаимодействия вихрей Абрикосова с дефектами кристалла, т.е. силой пиннинга – закрепления вихрей на структурных несовершенствах. ВТСП материалы имеют сравнительно низкую концентрацию носителей, что приводит к существенным отличиям в поведении их электрических и магнитных свойств. Мы уже говорили об этих особенностях (п. 1.7), ниже покажем, как влияют на плотность критического тока сильная анизотропия кристаллической структуры и физических свойств, аномально малая длина когерентности (ξ0), склонность к переходу металл – изолятор.
Склонность к фазовому переходу металл – изолятор характерна для металлоокисных соединений. Такие фазовые переходы сопровождаются исчезновением сверхпроводимости и могут происходить как при изменении температуры (T>Tс), так и при изменении концентрации компонентов (п. 2.5.1). Вследствие низкой концентрации носителей и анизотропии кристаллической структуры, металлический характер зонной структуры постоянно находится под угрозой, т. к. существование зон свободных носителей обусловлено вполне определенной координацией атомов меди и кислорода в слоях CuO2 и цепочках CuO. Любое нарушение этой координации ведет к локальному переходу металл – изолятор или металл – полупроводник. Поэтому структурные дефекты сильно снижают транспортные свойства металлоокисных ВТСП. Наиболее серьезным оказывается влияние планарных дефектов, пересекающих медь-кислородные слои (плоскости ab) кристаллов ВТСП. Это могут быть микротрещины, границы зерен, дислокационные стенки и двойниковые границы доменов с индексами (110). Вследствие малой длины когерентности, меньшей, чем толщина дефекта, дефект становится непрозрачным для транспорта электронов. Так, между зернами ВТСП возникают «слабые связи», которые ведут себя подобно джозефсоновскому контакту, а сам образец называют джозефсоновской средой. Поэтому и говорят о внутризеренной (jCG) и межзеренной (jCJ) критической плотности тока, причем jCG >> jCJ.
Высокие температуры перехода в сверхпроводящее состояние являются главной, наиболее привлекательной особенностью ВТСП материалов. Однако при достижении достаточно высоких температур тепловая энергия (~kT) становится сравнимой по величине с энергией пиннинга потока, что вызывает термически активированное движение вихрей Абрикосова путем перескока из одной потенциальной ямы в другую (крип потока). Этот процесс, в свою очередь, ограничивает транспортные свойства сверхпроводника.
ВТСП материалы можно разделить на три большие группы: монокристаллы, пленки и поликристаллические ВТСП. Последние, в свою очередь, по текстуре делятся на керамические и сплавленные монолитные образцы. Характер токопереноса в этих материалах сильно изменяется в соответствии с их структурными различиями.
Монокристаллы в этом ряду выделяются тем, что являются, по-видимому, самыми совершенными массивными объектами. Результаты, полученные на них, наиболее подлинны и доступны для понимания. Кроме того, вероятно, можно считать, что зерна поликристаллов подчиняются закономерностям, полученным для монокристаллических образцов.
Рассмотрим монокристалл ВТСП, включенный в цепь постоянного тока. На рис. 2.18 приведена вольт-амперная характеристика такой цепи.
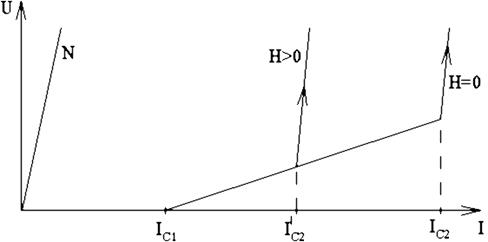
Рис. 2.18. Вольт-амперная характеристика разрушения сверхпроводимости током (схема)
При увеличении тока до IС1 падение напряжения на сверхпроводнике остается равным нулю. IС1 – первый критический ток, соответствующий началу перехода в нормальное состояние. На сверхпроводнике появляется падение напряжения, которое увеличивается при увеличении тока в цепи до IC2, когда переход в нормальное состояние заканчивается. Если на образец наложить магнитное поле (H>0), переход закончится при меньшем токе IC2’<IC2. График N соответствует ВАХ для нормального состояния образца (T>TС), и его наклон определяется сопротивлением материала.
В реальном кристалле критическое состояние четко не определено: при отличной от нуля температуре T всегда существует вероятность срыва абрикосовских вихрей, соответствующая термоактивизированному крипу потока. В результате, данные при значениях транспортного тока ниже критического, существует отличное от нуля напряжение, которое при низких температурах определяется выражением:
e=Bwd exp[-Ecp/kT(1-j/jc)], (2.13)
где j<jc – плотность транспортного тока;
e - напряженность электрического поля;
B – индукция магнитного поля;
w - характерная частота колебаний вихревой нити;
d – расстояние между центрами пиннинга;
Ecp - средняя энергия связи вихря на центре пиннинга.
Обычно, вклад в общее напряжение члена (2.13) мал, но при малых напряжениях его нужно учитывать, особенно, при определении IC1.Для описания поведения критической плотности тока в широком интервале температур используют эмпирическую зависимость:
jc(T)=jc(0)[exp(-T/T0)-exp(-Tc/T0)], (2.14)
где T0 – параметр ВТСП материала.
Выражение (2.14) имеет экспоненциальный характер при низких температурах и линейную зависимость в условиях (Tc-T)<<T0.
Как уже отмечалось, критический ток низкотемпературных сверхпроводников зависит от напряженности внешнего магнитного поля. Это справедливо и в случае ВТСП, однако зависимость является более сложной, поскольку материал анизотропен. В первом приближении можно воспользоваться выражением (2.15) с учетом того, что параметр B0 имеет разные значения для разных кристаллографических направлений и зависит от температуры.
Jс(0) = jс(0) exp(b-b0). (2.15)
В итоге, величину критической плотности тока удобнее записывать в виде тензора с учетом направления магнитного поля.
В поликристаллических образцах картина протекания транспортного тока оказывается сложнее, чем в монокристаллах, вследствие влияния межзеренных границ, хотя общие тенденции сохраняются. Мы уже говорили о существовании внутригранульной (jCG) и межгранульной (jCJ) плотностях критического тока. Эффективная критическая плотность jCJ оказывается на несколько порядков меньше чем jCG. Кроме того, температурные зависимости этих параметров оказываются тоже различными.
Для поведения jCG характерна так же, как и в случае монокристаллов, экспоненциальная зависимость (2.14), причем параметры jCG(0) и T0G оказываются близкими к параметрам монокристаллов. Температурная зависимость межгранульного тока близка к линейной при высоких температурах и насыщается при понижении температуры. Анализ зависимостей межгранульного тока более детально удается провести с помощью модели джозефсоновской среды.
Еще одной характерной особенностью межгранульного критического тока является его сильная зависимость от магнитного поля, что не удивительно, если вспомнить о характере действия поля на переход Джозефсона (п. 2.3). Для описания этой зависимости предложено выражение:
jCJ = jCJ(0)/(1+B2/B02). (2.16)
Для повышения критического тока керамики были использованы расплавные методы (п. 2.3). Применение этих технологий позволило существенно увеличить плотность критического тока. В частности, на рис. 2.19 приведена зависимость плотности критического тока от магнитного поля для метода QMG.
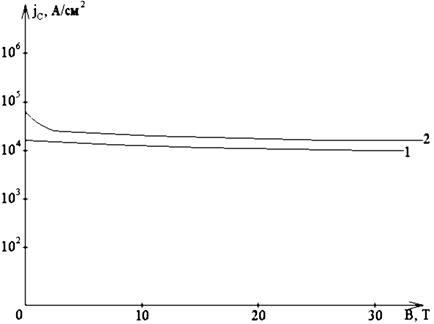
Рис. 2.19. Зависимость плотности тока от магнитного поля:
T=4,2 K; 1 – Y-123; 2 – Bi-2212
Хорошие результаты дают и другие расплавные технологии. Фирма IBM сообщила, что получает образцы, обладающие высокотемпературной сверхпроводимостью при плотности тока порядка 109 А/см2.
Характерной особенностью тонких пленок ВТСП является высокая плотность критического тока (105–107 А/см2) и слабая её зависимость от магнитного поля. Это относится к пленкам на основе Y-123, Bi-2223, Bi-2212, Tl-2212. Характер полевой зависимости аналогичен зависимости для монокристаллов.
На рис. 2.20 приведена температурная зависимость плотности критического тока для тонкой пленки Y-123.
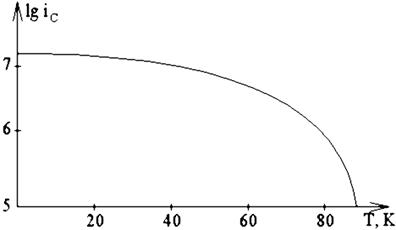
Рис. 2.20. Температурная зависимость плотности критического тока пленки Y-123
Температурная зависимость для тонких пленок оказывается более слабой, по сравнению с керамическим образцами. Было отмечено удовлетворительное согласие экспериментальной кривой на рис. 2.20 с зависимостью (2.15), полученной для монокристалла.
Очевидно, одна из причин высоких характеристик тонких пленок заключается в сходстве их текстур с текстурами монокристаллов. Кроме того, необходимо учитывать, что при малой толщине материал пленки более доступен для насыщения его кислородом.
Дата добавления: 2016-11-29; просмотров: 1952;











