Действие кратковременной нагрузки на систему с одной степенью свободы

Внезапно приложенная возмущающая сила постоянной величины. Если к упругой системе, находящейся в состоянии покоя, в момент времени t₀ прикладывается возмущающая сила P(t) = Р, то уравнение динамического равновесия без учета затухания для t> t₀ будет таким:

у" + w²у = Р/m. (20)

Полное решение этого уравнения, включающее свободные и вынужденные колебания системы при t₀ = 0, имеет следующий вид

у = а sin (wt + 𝜑₀) + [P/(mw²)] (1 — cos wt). (21)

Так как из формулы (13) w² = , то Р/(mw²) = у_СТ и динамический коэффициент силы Р при вынужденных колебаниях будет

μ = 1 — cos wt. (22)

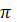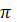Наибольшее значение этого коэффициента при wt= , З , ... достигает μ_max = 2.

На рис. 6 показан график колебательного движения точки приложения силы Р.

Рис. 6

Внезапно приложенная и внезапно прекратившая свое действие сила постоянной величины. Принимается, что сила Р прикладывается внезапно в момент времени t₀ и сохраняет постоянное значение в течение периода Т_р.

Для периода t₀ < t < t₀ + Т_р действительно предыдущее решение, а в период t>t₀ + Т_р, т. е. после прекращения действия силы Р, система будет совершать свободные колебания в соответствии с первым членом выражения (21). При этом начальные условия этого движения (при t =t₀ + Т_р), совпадающие с условиями движения в конце предыдущего периода, позволяют определить амплитуду колебаний и динамический коэффициент силы Р:

μ = ± 2 sin (wТ_р/2) = ± 2 sin ( 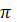Т_р/Т). (23)

Величина этого коэффициента от соотношения между периодом Т действия нагрузки и периодом Т свободных колебаний системы. В табл. 1 приведены значения μ в зависимости от величины Т_р/Т.

Таблица 1.

т_р/т 0,01 0,02 0,05 0,1 0,167 0,2 0,3 0,4 0,5 и более

μ 0,52 0,126 0,313 0,618 1,00 1,175 1,617 1,902 2,0

Кратковременный импульс силы. Если импульс сосредоточенной силы P(t) имеет величину S и действует в течение малого промежутка времени (периода) Т°_р, то среднее значение силы за этот период будет

P = S/T°_p. (24)

Приняв вместо силы P(t) ее среднее значение Р, можно воспользоваться формулой (23) для динамического коэффициента. Обе части этого выражения умножим на Р и, кроме того, правую часть умножим и одновременно разделим на wТ⁰_р. Тогда в левой части получим статическую силу, эквивалентную данному импульсу по своему действию.

Так как для любого угла 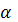отношение sin 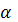/ 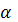< 1 и это отношение при стремлении 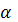к нулю стремится к единице, то наиболее опасным из всех ударных импульсов, имеющих заданную величину S, является мгновенный импульс, для которого:

Р_эк = 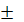wS (25)

Ударная нагрузка. При ударе движущегося тела по упругой системе, например в случае свободного падения груза Q = mg на конец балки, происходит передача кинетической энергии движения груза балке, сопровождающаяся деформацией последней и возникновением равных между собой сил взаимодействия груза и балки. Каждая из этих сил называется силой удара. Сила удара имеет вполне определенную продолжительность, или период действия, Т_р°, обычно измеряющийся сотыми или тысячными долями секунды, и в течение этого периода изменяется по

величине. Примерный график силы удара показан на рис. 7 (сплошная линия).

Сила удара характеризуется ее наибольшей величиной Р, периодом Т°_ри импульсом, равным площади диаграммы удара:

S = 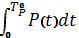. (26)

В то же время импульс силы удара равен количеству движения ударяющей массы m:

S = mv,

где v— скорость движущейся массы т.

Если сила в течение периода Т_р остается постоянной и равной Р, то импульс такой силы будет выражаться простым произведением:

S = РТ_р. (27)

Сила удара, период ее действия и закон изменения во времени зависят не только от величины массы тела и скорости его движения, но также и от упругих свойств самого сооружения и его поверхности в месте удара. В настоящее время мы можем получить график силы удара только экспериментальным путем, например с помощью осциллографа. График силы удара можно приближенно заменить равновеликим прямоугольником, например, исходя из равенства наибольших ординат, как это показано на рис. 7 штриховой линией, или исходя из равенства периодов Т_р = Т°_р.

Не зная периода действия ударной нагрузки, будем считать ее импульс мгновенным. Тогда эквивалентная статическая сила выразится формулой (25).

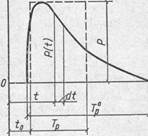
Рис. 7

Эффект ударной нагрузки зависит не только от величины ее импульса, но также и от частоты собственных колебаний самой системы. Чем жестче сооружение, тем больше будет динамический коэффициент удара при одном и том же импульсе.

Дата добавления: 2016-11-29; просмотров: 1994;