Метод последовательных приближений

Пусть некоторая система состоит из N=8 последователь­но включенных элементов.

Предположим, что вероятности отказов элементов равны, т. е. появление отказа любого элемента равновероятно.

Вероятность обнаружения отказавшего элемента методом поочередных случайных испытаний равна ¹/7. Это значит, что время обнаружения отказа пропорционально числу элементов без одного (последний элемент не испытывается);

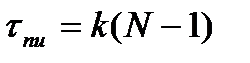, (11.12)

где k — среднее время проведения одного испытания;

τ_пи — время обнаружения методом поочередных испы­таний.

Метод последовательных приближений в частном случае, когда мы не располагаем предварительной информацией (признаками нормальной работы до испытаний), может быть сведен к так называемому методу средней точки. Это значит, что мы производим первое испытание в середине системы между элементами 4 и 5. В результате границы неисправного участка системы сокращаются до элементов 5, 6, 7 и 8. Сразу исключается из рассмотрения исправная половина системы (элементы 1, 2, 3 и 4).

Второе испытание делит пополам оставшийся неисправ­ным участок системы. Таким образом, для отыскания неис­правного элемента в системе, состоящей из восьми элементов, необходимо произвести не более трех испытаний.

Максимальное число испытаний т при таком методе под-считывается по формуле

Время обнаружения неисправного элемента

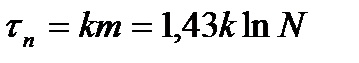
Метод последовательных приближений является необхо­димым, но не достаточным элементом методики. Для его реа­лизации нужны определенные приемы (способы) испытаний.

Основными способами испытаний являются:

— способ контрольных переключений и регулировок;

— способ промежуточныхизмерений;

— способ замены;

— способ внешнего осмотра;

— способ сравнения;

— способ характерных неисправностей.