Электрооптические модуляторы

В настоящее время наиболее распространенным электрооптическим модулятором является модулятор на ячейке Поккельса. Принцип действия модуляторов на ячейке Поккельса основан на линейном электрооптическом эффекте, который заключается в изменении показателя преломления среды пропорционально приложенному электрическому полю.

Линейный электрооптический эффект
в одноосных кристаллах

Для оптически однородного анизотропного кристалла зависимость относительной диэлектрической проницаемости от направления может быть представлена графически. Если из произвольной точки О кристалла проводить по всевозможным направлениям радиус-векторы r, модули которых r=(e)^1/2 , где e - относительная диэлектрическая проницаемость кристалла в направлении r, то концы векторов r будут лежать на поверхности эллипсоида, называемого оптической индикатрисой(рис.5.1).

Рис.5.1. Оптическая индикатриса анизотропного кристалла.

Оси симметрии эллипсоида определяют три взаимно перпендикулярных главных направления в кристалле. В прямоугольной декартовой системе координат, оси OX, OY и OZ которой проведены вдоль главных направлений, уравнение оптической индикатрисы любого кристалла в главной системе координат имеет вид:

a₁₀x² +a₂₀y² +a₃₀z² =1, (5.1)

где a₁₀, a₂₀, a₃₀ – коэффициенты, соответствующие главным осям значения обратных величин диэлектрических проницаемостей;

a₁₀ = 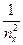, a₂₀= 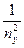, a₃₀= 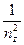, (5.2)

n_x, n_y, n_z - показатели преломления вдоль главных осей.

Линейный электрооптический эффект описывается линейным изменением коэффициентов оптической индикатрисы кристалла при приложении электрического поля.

При приложении электрического поля эллипсоид оптической индикатрисы (5.1.) поворачивается и деформируется. Главные оси данного эллипсоида в общем случае не будут совпадать с исходными главными осями. Уравнение оптической индикатрисы в системе координат XYZ примет вид: a₁x²+a₂y²+a₃z²+2a₄yz+2a₅zx+2a₆xy=1. (5.3)

В случае линейного электрооптического эффекта изменение коэффициентов индикатрисы: 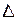_k=a_k-a_k0 линейно связано с приложенным полем, соотношением: a_k-a_k0=r_k1Е_x+r_k2Е_y+r_k3Е_z, (5.4)

где k=1,2,..,6; a₄₀=a₅₀=a₆₀=0.

Коэффициенты r_kn образуют тензор третьего ранга, называемый электрооптическим тензором.

В современных электрооптических модуляторах света наиболее широко применяются одноосные кристаллы, принадлежащие классам 42m (дигидрофосфат амония-ADP, калия-KDP и их дейтерированные модификации-DKDP, DAPD), 4mm (титанат бария - BaTiO₃) и 3m (ниобат лития-LiNbO₃).

Для кристаллов класса 42m из 18 компонент тензора [r_kn] не равны нулю лишь три: r₅₂=r₄₁ и r₆₃, а у кристаллов класса 3m - r₁₃=r₂₃, r₃₃, r₄₂=r₅₁, r₂₂=-r₁₂=-r₆₁.

Для одноосных кристаллов коэффициенты в уравнении (5.1) равны: a₁₀=a₂₀=1 /n_о², a₃₀ =1 /n_e², где n_о и n_e - показатели преломления для обыкновенной и необыкновенной волн.

В зависимости от взаимной ориентации направления электрического поля и волнового вектора света различают поперечный и продольный электрооптический эффекты. Если направление электрического поля и волнового вектора света взаимно перпендикулярны, то электрооптический эффект называется поперечным. Если эти направления параллельны, то электрооптический эффект называется продольным.

Допустим, что электрическое поле в кристалле класса 42m направлено вдоль оси OZ, совпадающей с оптической осью кристалла, т.е.E_x=E_y=0, E_z=E,, тогда из (5.3) с учетом (5.4) имеем: a₁₀(x²+y²)+a₃₀z²+2r₆₃Exy=1 (5.5)

При отсутствии электрического поля сечение оптической индикатрисы плоскостью Z=0 представляет собой окружность (рис. 5.2).

Приложение электрического поля деформирует этот круг в эллипс с главными осями OX' и OY', как показано на рис. 5.2.

Показатели преломления вдоль новых осей OX' и OY' уже зависят от напряженности электрического поля E:

n_x'=1/(a₁₀-r₆₃E)^1/2»n₀+1/2(n₀³r₆₃E) (5.6 a)

n_y'=1/(a₁₀+r₆₃E)^1/2»n₀-1/2(n₀³r₆₃E) (5.6 б)