Системы координат, принятые в геодезии

В геодезии применяются следующие системы координат:

· Географическая система координат

· Зональная система плоских прямоугольных координат Гаусса–Крюгера,

· Полярная система координат.

4.1. Географические координаты

С помощью географических координат, то есть широт (φ) и долгот (λ), определяют положение точки относительно экватора и начального меридиана.

Широтой (φ) точки называется угол, составленный отвесной линией в данной точке и плоскостью экватора.

Долготой(λ) точки называется двугранный угол между плоскостью меридиана данной точки и плоскостью начального меридиана.

Широта отсчитывается по дуге меридиана к северу и к югу от экватора от 0º до 90º. К северу от экватора широта называется северной, к югу – южной.

Долгота отсчитывается от меридиана, проходящего через Гринвич на окраине Лондона. Долгота отсчитывается по дуге экватора или параллели от начального меридиана в сторону востока и запада от 0º до 180º. Долгота к востоку от Гринвичского меридиана называется восточной долготой, к западу – западной. Широты и долготы определяют положение любой точки на земной поверхности и выражаются в угловой мере. Географические координаты определяются из астрономических наблюдений и, а также с помощью геодезических измерений.

4.2. Зональная система плоских прямоугольных координат Гаусса–Крюгера

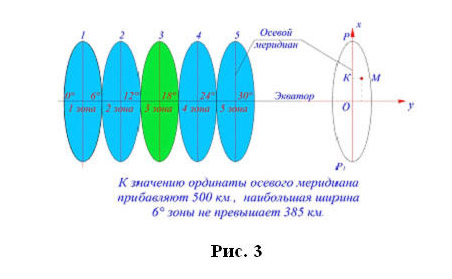
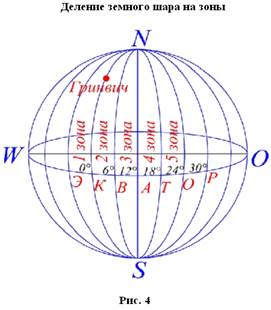
При геодезических работах на больших территориях применяется зональная система плоских прямоугольных координат Гаусса–Крюгера(рис. 3). Для этого земной шар делится меридианами на шестиградусные или трехградусные зоны (рис. 4). Счет зон ведется к востоку от Гринвичского меридиана. Каждая зона проецируется на плоскость таким образом, чтобы средний меридиан зоны был изображен прямой линией. Средний меридиан зоны называется осевым.

Изображение осевого меридиана принимается за ось абсцисс, изображение экватора – за ось ординат. За начало координат принимают точку пересечения осевого меридиана с экватором.

Чтобы не иметь отрицательных ординат, ординату осевого меридиана принимают равной 500 км. Перед ординатой точки указывается номер зоны, в которой точка расположена.

Зональная система плоских прямоугольных координат
Гаусса–Крюгера

Зная географические координаты точки земной поверхности, можно вычислить зональные прямоугольные координаты, и, наоборот.

4.2. Полярная система координат

В полярной системе координат используются полярные углы и расстояния. Подробнее эта система будет рассмотрена в последующих лекциях.

5. Системы высот, принятые в геодезии

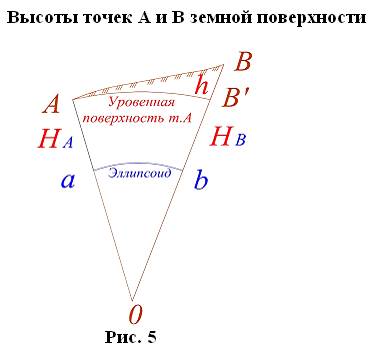
Для полного определения положения точек земной поверхности необходимо знать высоты точек над принятой уровенной поверхностью. Высоты точек, которые определяются относительно поверхности эллипсоида (по отвесной линии), называются абсолютными высотами.

Абсолютная высота – длина перпендикуляра, опущенного из точки на уровенную поверхность, принятую за начало отсчета (поверхность эллипсоида).

За начало счета абсолютных высот принимается нуль Кронштадтского футштока (средний уровень воды в Балтийском море). Такая система высот называется Балтийской.

Уровень Балтийского моря установленный по данным многолетних наблюдений и отмеченный награвированной чертой на металлической пластине, вмурованной в гранитный устой одного из мостов через обводной канал в Кронштадте, является началом счета высот уже третий век. Если счет высот ведется от другой уровенной поверхности, такая высота называется относительной высотой.

Числовые значения абсолютных высот точек земной поверхности называют отметками. Разность абсолютных высот двух любых точек называют превышением (h).

В строительстве для отдельных зданий счет высот ведется от чистого пола первого этажа.