Проблема оврагов. Метод покоординатного спуска

К сожалению, выбор антиградиента в качестве направления спуска не всегда является удачным. Особенно ярко это проявляется для овражных функций.

Градиентный метод сходится достаточно быстро, если для минимизируемой функции поверхности уровня близки к сферам (при m=2 линии уровня близки к окружностям).

Действительно, известно, что градиентный метод сходится очень медленно, если поверхности уровня минимизируемой функции сильно вытянуты в некоторых направлениях.

В двумерном случае рельеф соответствует поверхности U=Q(x₁,x₂) и напоминает рельеф местности с оврагом. Поэтому такие функции называют «овражными» (рис.1.8.5-1).

Рис. 1.8.5-1

Вдоль направлений, характеризующих «дно оврага», «овражная» функция меняется незначительно, а в других направлениях, характеризующих «склон оврага», происходит резкое изменение значений функции.

Если начальная точка Х₀ попадает на «склон оврага» , то направление градиентного спуска оказывается почти перпендикулярным «дну оврага» и очередное приближение Х₁ попадает на противоположный «склон оврага».

Следующий шаг в направлении ко «дну оврага» возвращает приближение Х₂ напротивоположный «склон оврага» и т.д.

В результате вместо того, чтобы двигаться вдоль оврага (в направлении точки минимума), траектория спуска совершает зигзагообразные скачки поперек «оврага».

Один из существенных недостатков градиентного метода связан с его чувствительностью к погрешностям вычислений. Особенно сильно этот недостаток сказывается в малой окрестности точки минимума, где антиградиент, задающий направление поиска, мал по модулю. Поэтому эффективность градиентного метода на завершающей стадии существенно ниже, чем на начальной.

Проблему «оврагов» позволяют решать специально разработанные «овражные» и другие методы спуска, например, метод покоординатного спуска.

В методе покоординатного спуска в качестве очередного направления спуска выбирают направление одной из координатных осей. Наиболее известным является метод циклического покоординатного спуска.

Рассмотрим очередной n+1 цикл одного из вариантов этого метода, считая, что приближение к минимуму функции Q(X)=Q(x₁, … x_m) уже найдено Х_n.

1-й шаг. На первом шаге проводят спуск по координате x₁. Значения остальных координат x₂ = x₂⁽ⁿ⁾ , x₃ = x₃⁽ⁿ⁾ , … , x_m= x_m⁽ⁿ⁾ фиксируют, а x₁⁽ⁿ⁾ выбирают из условия:

Q(x₁⁽ⁿ⁺¹⁾ , x₂⁽ⁿ⁾ … x_m⁽ⁿ⁾ ) = min Q(x₁, x₂⁽ⁿ⁾ … x_m⁽ⁿ⁾ )

x₁

Фактически решается задача минимизации функции одной переменной.

Q(x1) = min Q(x1, x2(n) … xm(n) ).

2-шаг. На втором шаге производится спуск по координате x₂. Значения остальных координат x₁ = x₁⁽ⁿ⁾ , x₃ = x₃⁽ⁿ⁾ , … , x_m= x_m⁽ⁿ⁾ фиксируют, а x₂⁽ⁿ⁺¹⁾ выбирают как решение задачи одномерной оптимизации

Q(x₁⁽ⁿ⁺¹⁾ , x₂⁽ⁿ⁺¹⁾ , x₃⁽ⁿ⁾ … x_m⁽ⁿ⁺¹⁾ ) = min Q(x₁⁽ⁿ⁺¹⁾, x₂, x₃⁽ⁿ⁾ … x_m⁽ⁿ⁾ ).

x₂

Аналогично осуществляют следующие шаги.

m-й шаг. На последнем шаге координату x_m⁽ⁿ⁺¹⁾ определяют из условия

Q(x₁⁽ⁿ⁺¹⁾ , x₂⁽ⁿ⁺¹⁾ , … x_m-1⁽ⁿ⁺¹⁾,x_m⁽ⁿ⁺¹⁾ ) = minQ(x₁⁽ⁿ⁺¹⁾, … x_m-1⁽ⁿ⁺¹⁾,x_m).

x₂

В результате получается очередное приближение x⁽ⁿ⁺¹⁾ к точке минимума.

Далее цикл метода снова повторяется. Каждый цикл метода состоит из m шагов (т.е. по количеству переменных). Т.к. на k-том шаге очередного цикла значение координаты x_k⁽ⁿ⁺¹⁾ определяют из условия минимизации функции f по направлению x_k, то необходимо, чтобы в точке (x₁⁽ⁿ⁺¹⁾ , x₂⁽ⁿ⁺¹⁾ , … x_k-1⁽ⁿ⁺¹⁾, x_k, x_k+1⁽ⁿ⁺¹⁾ , …x_m⁽ⁿ⁺¹⁾) производная 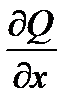обращалась в ноль.

На рисунке изображена графическая иллюстрация циклического покординатного спуска для случая m=2.

Рис. 1.8.5-2

Рис.1.8.5-3. Схема алгоритма метода наискорейшего спуска