Метод градиентного спуска с дроблением шага

На каждой итерации шаг спуска l_k выбирается таким образом, чтобы выполнялось условие:

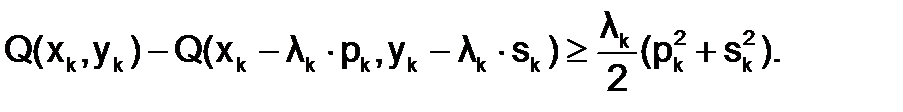(1.8.3-1)

Выбор шага в методе ГДШ заключается в следующем.

Задается начальное значение шага l_k = l₀ (как правило, l₀=0,5). Проверяется условие сходимости, приведенное выше. Если условие сходимости выполняется, то шаг спуска для данной итерации выбран, а если оно не выполняется, то принимают новый шаг l_k = l_k/2, и снова проверяют условие сходимости (и т.д.).

Алгоритм метода ГДШ можно описать следующей последовательностью действий:

1.При k = 0 задаемся начальной точкой спуска (x_k, y_k), требуемой точностью e и начальным шагом l₀(пусть l₀ =0,5).

2.Вычисляем значения

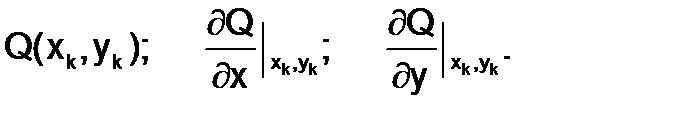(1.8.3-2)

3.Вычисляем новые значения переменных

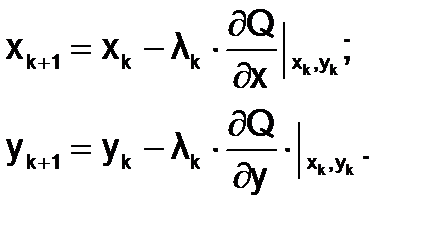(1.8.3-3)

4.Проверяем условие сходимости:

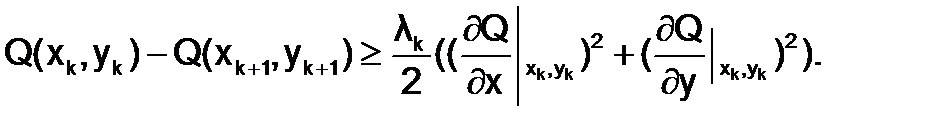(1.8.3-4)

Если условие выполняется, то полагаем величину шага равной l_k, в противном случае l_k = l_k/2 и переходим к п.3.

5.Проверка окончания процесса итераций (необходимого условия существования минимума):

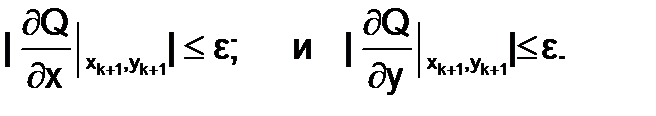(1.8.3-5)

Если условие выполнено, то минимум найден, а если нет - вычисление координат следующей точки (k=k+1) и передача управления п.2.

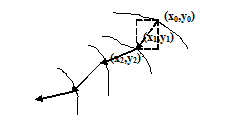
Рис. 1.8.3-1. Траектория спуска ГДШ

Алгоритм выбора шага в градиентном методе дробления шага приведен на
рис. 1.8.3-2.

Рис. 1.8.3-2. Схема алгоритма выбора шага в градиентном методе дробления шага