Способы задания прямоугольной системы координат

Как известно, система прямоугольных координат на плоскости может задаваться тремя способами:
1-й способ

фиксируется местоположение центра системы - т.O,

проводится ось OX и указывается ее положительное направление,

перпендикулярно к оси OX проводится ось OY,

в соответствии с типом системы (правая или левая) указывается положительное направление оси OY,

устанавливается масштаб координат вдоль осей.

При наличии координатных осей для определения координат какой-либо точки C нужно сначала опустить перпендикуляры из этой точки на координатные оси и затем измерить длину этих перпендикуляров; длина перпендикуляра к оси OX равна координате Y, длина перпендикуляра к оси OY координате X точки (рис.2.1).

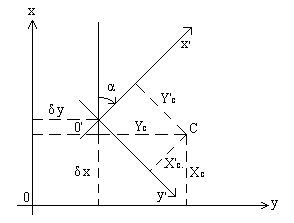
Рис.2.1

Кроме системы XOY можно использовать систему X'O'Y', получающуюся из системы XOY путем переноса начала координат в точку O' ( Xo'=δx , Yo'= δy ) и поворота осей координат по часовой стрелке на угол α.
Переход из XOY в X'O'Y' выполняется по формулам [25]:

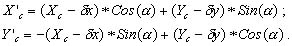(2.1)

Для обратного перехода используются формулы [25]:

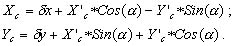(2.2)

2-й способ

проводятся две взаимно перпендикулярные системы параллельных линий; расстояния между линиями одинаковые,

считается, что эти линии параллельны осям координат, и у каждой линии подписывается значение соответствущей координаты (получается координатная сетка).

3-й способ

указываются численные значения координат двух фиксированных точек.

Первый способ является общепринятым; в геодезии этим способом задается зональная система прямоугольных координат Гаусса.

На топографических картах и планах система прямоугольных координат Гаусса задается вторым способом.

На местности система прямоугольных координат задается третьим способом; всегда можно найти несколько геодезических пунктов с известными координатами и определять положение новых точек относительно этих пунктов, выполняя какие-либо измерения.