Метод разложения решения в ряд Тейлора
Метод Эйлера
Пусть требуется решить уравнение вида 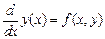 для заданных начальных условий:
для заданных начальных условий: 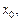
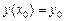 численно методом конечных разностей.
численно методом конечных разностей.
Число точек дискретизации: 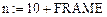
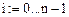
Задание функции: 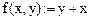
Область определения функции: 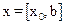
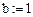
Начальные условия: 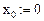
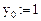
Просмотр на экране дисплея численного значения функции в этой точке: 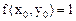
Дискрет по х: 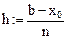 . Для выбранных параметров
. Для выбранных параметров 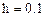
Дискретное представление самой переменной: 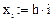
Таким образом, для вычисления у(х) получим выражение
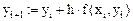 (2)
(2)
Приведем некоторые его значения: 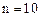
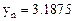
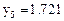
Точное решение этого дифференциального уравнения: 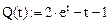
Значение функции на правой границе: 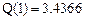 (рис. 1; возможна анимация графика по параметру n).
(рис. 1; возможна анимация графика по параметру n).
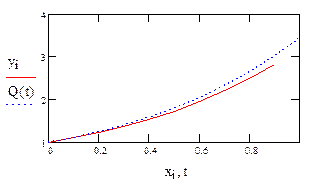
Рис. 1
Разностная схема (метод) не всегда работает. Если 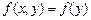 и
и 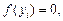 то в силу (2) значения
то в силу (2) значения 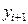 будут равны
будут равны 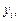 что не всегда так. Примером может служить процесс, описываемый уравнением
что не всегда так. Примером может служить процесс, описываемый уравнением 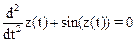 или уравнением
или уравнением 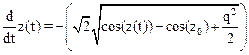
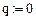
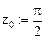 с заданными начальными условиями:
с заданными начальными условиями: 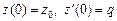 . Независимо от значения q,
. Независимо от значения q, 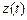 — изменяемая во времени функция. Однако при q = 0 разностная схема дает другой результат:
— изменяемая во времени функция. Однако при q = 0 разностная схема дает другой результат: 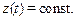 При
При 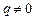 картина получается достоверной.
картина получается достоверной.
Если не ввести обозначение константы, то возникнут трудности при записи функции 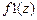 :
:
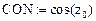
Пусть переменные z и t принадлежат соответственно интервалам 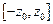 и
и 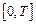 . Запишем переменную t в дискретном виде (значение Т подобрано как полупериод):
. Запишем переменную t в дискретном виде (значение Т подобрано как полупериод):
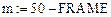
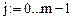
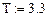
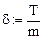
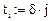
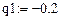

Рис. 2
Введем обозначение 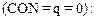
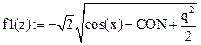
При этом (2) может быть записано в виде первых двух слагаемых ряда Тейлора:
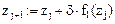
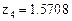
В результате получаем ошибочное решение zj, представляемое на графике прямой линией (рис. 2; возможна анимация графика).
В то же время при 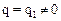 будем иметь:
будем иметь:
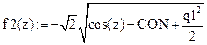
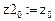
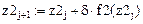
Это решение также представлено на рис. 2 и является единственно правильным.
Задания. 1. Снять клип по параметру q1: 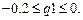
2. Привести другие примеры неадекватной работы метода Эйлера.
Метод Адамса
Решить уравнение вида 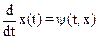 для заданных начальных условий:
для заданных начальных условий: 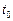 ,
, 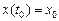 ,
, 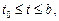 численно методом конечных разностей.
численно методом конечных разностей.
Запишем формулу Адамса с четырьмя членами [2]:
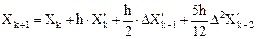
Здесь 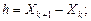
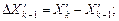
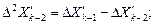
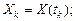
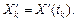
Формула Адамса дает возможность по 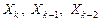 определить
определить 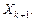 Таким образом, зная
Таким образом, зная 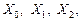 мы можем определить
мы можем определить 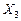 и далее
и далее 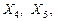 …
…
Рассмотрим на примере задачи, решенной выше, — см. подразд. 1.1 — моделирование алгоритма Адамса в системе MathCAD.
Дано: 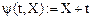
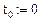
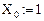
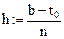
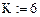
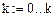
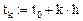
Просмотр численного значения: 
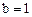
Вычисляем значение n-й производной: 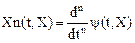 .
.
В системе Maple достаточно предыдущей символьной записи, а
в MathCAD каждую производную надо записывать отдельно.
Вторая производная: 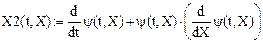
Третья производная:
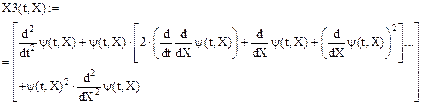
Запись последующих производных в MathCAD становится обременительной. В Maple эту процедуру символьного дифференцирования выполняет сама система, что позволяет записывать производные практически любого порядка и работать с ними.
Можно осуществить проверку правильности вычисления производных для выбранных значений функции в отдельных точках: 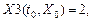
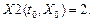
Вывод: вычисление в среде MathCAD выполнено правильно, в том числе и для других функций.
Введем обозначения: 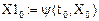
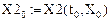
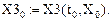
Просмотр численных значений и проверка: 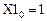
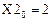
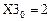
Проверка завершена успешно.
Используя разложение 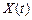 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 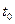 и беря его первые четыре члена, определим
и беря его первые четыре члена, определим 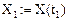 и
и 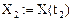 как
как
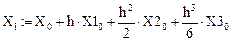
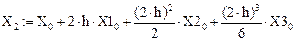
Проверка численных значений:
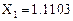
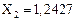
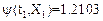
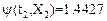
Первые разности:
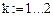
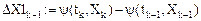
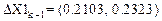
Вторые разности:
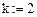
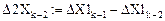
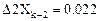
Проверка завершена успешно.
Далее все последующие значения х будем вычислять по формуле Адамса, имеющей вид
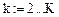
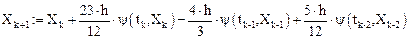
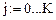
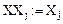
Результаты вычислений представим в виде вектора X и графически (рис. 3):
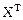 = (1 1.1103 1.2427 1.3995 1.5833 1.7969 2.0435 2.3266)
= (1 1.1103 1.2427 1.3995 1.5833 1.7969 2.0435 2.3266)
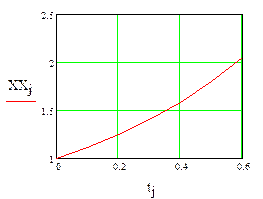
Рис. 3
Сравним численные результаты, полученные разными методами: метод Эйлера — 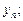 метод Адамса —
метод Адамса — 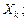 точное решение —
точное решение — 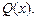
Значение в точке 0.4: 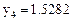
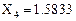
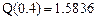
Относительная ошибка в процентах:
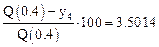
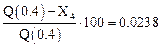
Значение в точке 0.6: 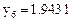
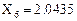
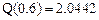
Относительная ошибка в процентах:
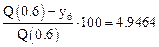
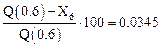
Метод разложения решения в ряд Тейлора
В основе метода, который также можно назватьметодом припасовывания, лежит представление решения рядом Тейлора. Решение должно быть гладким и иметь непрерывные производные до (n + 1)-го порядка включительно. Ряд Тейлора заменяется его первыми n + 1 членами разложения в окрестности точки tk на каждом участке k. Конечные значения аргументов на этом участке становятся начальными на следующем участке k + 1 (подробнее см. [3]).
На примере рассмотренного ранее уравнения 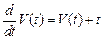 с начальными условиями:
с начальными условиями: 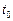 ,
, 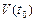 покажем, как работает этот метод.
покажем, как работает этот метод.
Дано: 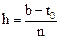
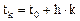
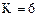
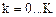
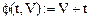
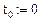
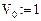
Вычисляем: 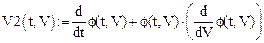
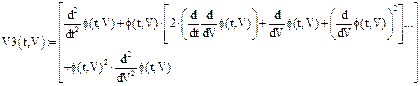
Проверка: 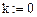
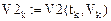
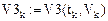
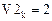
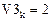
Численные значения производных в заданных точках подтверждены. Проверка завершена успешно.
Представим алгоритм вычислений (некоторые параметры следует переопределить еще раз): 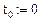
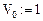
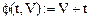
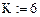
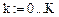
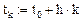
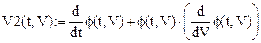
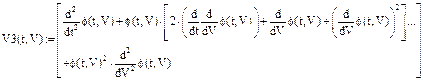
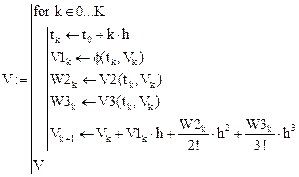
1.4. Сравнительный анализ численных результатов,
полученных разными методами
Имеются следующие результаты: метод припасовывания — 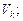 метод Адамса —
метод Адамса — 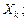 точное решение —
точное решение — 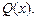
Необходимо переопределить имя компоненты вектора:
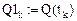
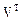 = (1 1.1103 1.2428 1.3998 1.5838 1.7968 2.0448 2.3284)
= (1 1.1103 1.2428 1.3998 1.5838 1.7968 2.0448 2.3284)
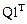 = (1 1.1103 1.2428 1.3997 1.5836 1.7974 2.0442)
= (1 1.1103 1.2428 1.3997 1.5836 1.7974 2.0442)
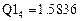
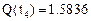
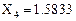 k: = 4
k: = 4
Относительная ошибка в процентах:
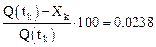
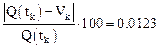
Замечание.Недопустимо определение 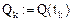 ! Формула в тексте далее идет как исполняемая формула! Переместите формулу выше и убедитесь в этом.
! Формула в тексте далее идет как исполняемая формула! Переместите формулу выше и убедитесь в этом.
Таким образом, метод припасовывания дает более точный результат, чем все предыдущие.
Упражнение 1.1
Решить численно дифференциальное уравнение второго порядка 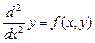 методом припасовывания для заданных функций:
методом припасовывания для заданных функций: 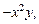
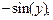
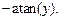 Здесь функция
Здесь функция 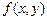 не содержит производной
не содержит производной 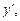 что упрощает алгоритм решения.
что упрощает алгоритм решения.
Дано: 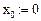
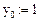
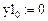
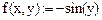
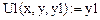
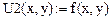
Если хотите сравнить полученное Вами решение с ответом, откройте в электронной версии методических указаний представленную ниже закрытую область.
Приступаем к решению, вычисляем. Третья производная: 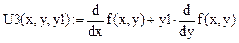
Четвертая производная:
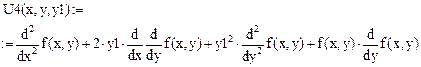
Зададим дискрет по x: 
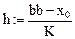
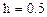
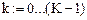
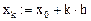
Алгоритм решения дифференциального уравнения:
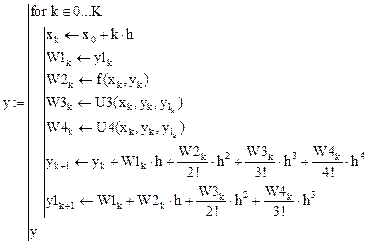
Дискретные значения первой производной от полученного решения y (рис. 4, 5, возможна анимация графиков):
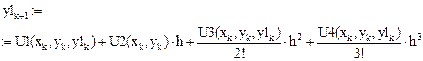
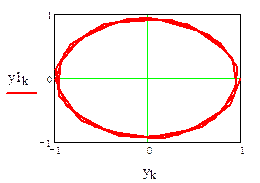
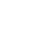 Рис. 4
Рис. 4
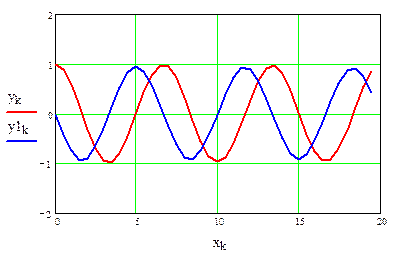
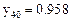
Рис. 5
Упражнение 1.2
Решить численно дифференциальное уравнение второго порядка 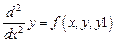 методом припасовывания, где
методом припасовывания, где
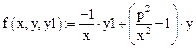
Это уравнение Бесселя (содержит 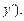 Здесь р = const,
Здесь р = const, 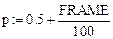 y' = y1
y' = y1
Дано: 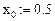
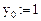
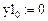
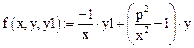
Первая и вторая производные заданы:
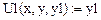
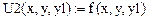
Третья производная:
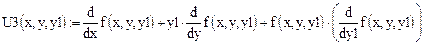
Четвертая производная:
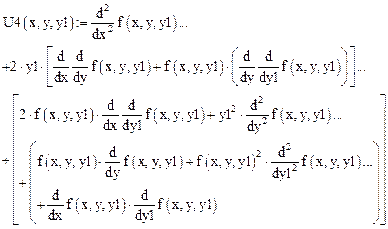
Зададим дискрет по x: 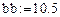
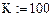
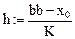
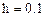
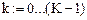
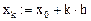
Если хотите сравнить полученное Вами решение с ответом, откройте в электронной версии методических указаний закрытую область.
Аналитическое выражение решения y(x) на участке припасовывания k, где 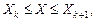 можно записать в виде
можно записать в виде 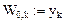
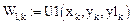
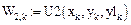
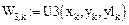
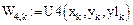
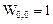
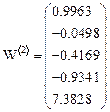
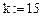
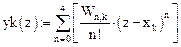 (3)
(3)
В качестве проверки (3) вычислим (здесь невозможны обозначения y(z), yk(x)):
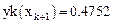
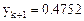
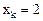
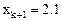
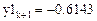
Учитывая, что 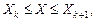 можно (3) переписать (
можно (3) переписать ( 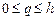 ):
):
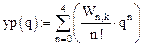
Результаты представим графически (рис. 6).
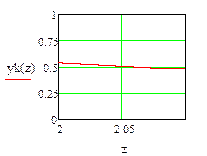
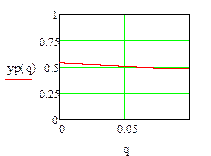
Рис. 6
Упражнение 1.3
Обобщить и записать в векторно-матричной форме алгоритм решения дифференциального уравнения второго порядка 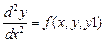 методом припасовывания на примере решения уравнения Бесселя.
методом припасовывания на примере решения уравнения Бесселя.
Дано: 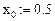
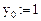
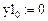
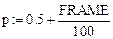
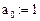
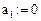
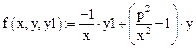
Введем обозначения: 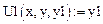
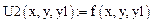
Порядок дифференциального уравнения: 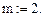
Старший порядок производной в разложении в ряд Тейлора: 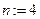
Зададим дискрет по x: 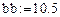
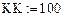
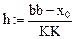
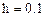
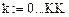
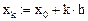
Начальные условия будем записывать в матрицу: {Yj,k} 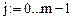
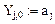
Матрица коэффициентов ряда Тейлора: 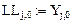
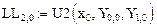
Третья производная:
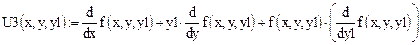
Четвертая производная:
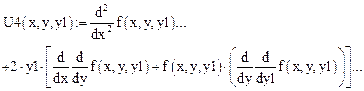
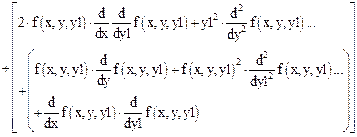
Если хотите сравнить полученное Вами решение с ответом, откройте в электронной версии методических указаний закрытую область.
Алгоритм:
|
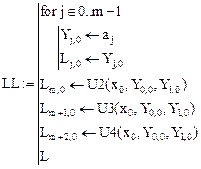
|
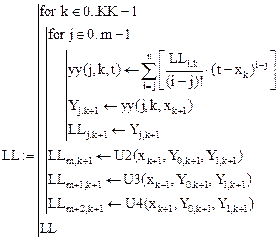
Ниже представлена матрица LL коэффициентов ряда Тейлора:
| 0.9995 | 0.9963 | 0.9892 | 0.9772 | 0.9601 | 0.9378 | |||
| -0.0147 | -0.0498 | -0.0949 | -0.1449 | -0.1967 | -0.2488 | ||||
| -0.2809 | -0.4169 | -0.4841 | -0.5146 | -0.5233 | -0.5179 | ||||
| -4 | -1.8816 | -0.9341 | -0.4513 | -0.1771 | -5.8968×10-3 | 0.1103 | |||
| 14.2205 | 7.3828 | 4.3536 | 2.8588 | 2.053 | 1.5835 |
Аналитический вид решения исходного дифференциального уравнения записан ниже ( j — порядок производной; k — участок припасовывания; t — независимая переменная):
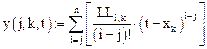
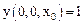
Фазовый портрет полученного решения представлен на рис. 7 (возможна анимация графика, 100 кадров).
Рис. 7
Анимация графика (рис. 8) показывает, что есть две устойчивые точки (два узла), которые практически не меняют своего положения при изменении параметра h. Это точки Х = 2 и Х = 4. Возможно, есть и другие точки.
Аналитическое выражение решения y(j, k, t) на участке припасовывания k, где 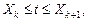 можно записать в виде
можно записать в виде
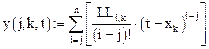
Графики участка припасовывания и всего процесса можно сопоставить на одном рисунке (рис. 9).
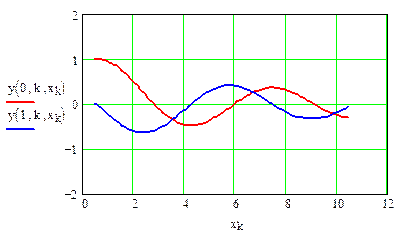
Рис. 8
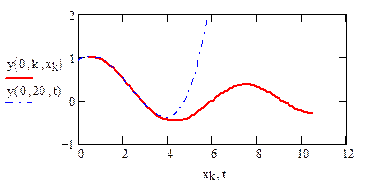
Рис. 9
 |
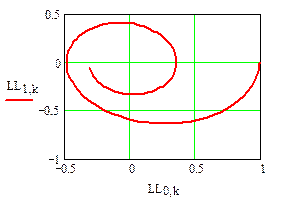
Рис. 10
Рис. 11
Другие возможности представления графиков решения исходного дифференциального уравнения иллюстрируют рис. 10 и 11.

Дата добавления: 2021-02-19; просмотров: 646;











