Метод интегральных соотношений

Метод интегральных соотношений, предложенный Г.И. Баренблаттом, по аналогии с методом пограничного слоя в потоке вязкой жидкости, позволяет получить приближенные решения некоторых задач нестационарной фильтрации упругой жидкости с нужной точностью.

Основные особенности метода Г.И. Баренблатта рассмотрим на примере неустановившегося плоскорадиального притока жидкости к скважине после ее пуска в эксплуатацию. В этом случае распределение пластового давления в возмущенной области вокруг скважины представляется в виде многочлена по степеням координаты r с коэффициентами, зависящими от времени, т.е.

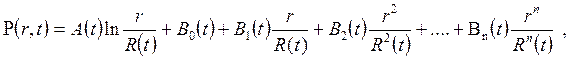(7.67)

.

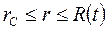Задача сводится к нахождению коэффициентов А, B₀, B₁, B₂,...., B_n, которые должны удовлетворять граничным условиям, т.е. условиям на стенке скважины и на внешней границе возмущенной области. Кроме того эти коэффициенты должны удовлетворять выведенным Г.И. Баренблаттом особым интегральным соотношениям. Число этих интегральных соотношений зависит от показателя степени n, а следовательно, от числа членов многочлена, входящего в уравнение (7.67). Показатель степени n в свою очередь выбирается в зависимости от желательной степени точности решения задачи. Чем больше число n, тем выше точность решаемой задачи. Г.И.Баренблат показал, что если принять n=0 (в этом случае интегральное соотношение сводится к уравнению материального баланса), то из его метода, как частный случай, получается метод последовательной смены стационарных состояний (ПССС).

Если принять n=1, то из метода Баренблатта вытекает, как частный случай, метод А.М.Пирвердяна; в этом легко убедиться, положив в уравнение (7.67) n=1 и сравнив его с уравнением (7.66).