Метод А.М. Пирвердяна

Этот метод аналогичен методу ПССС и уточняет его. В методе А.М. Пирвердяна, как и в методе ПССС неустановившийся фильтрационный поток в каждый момент времени мысленно разбивается на две области – возмущенную и невозмущенную. Граница между этими областями также определяется из уравнения материального баланса. Но в отличие от метода ПССС распределение давления в возмущенной области по методу А.М.Пирвердяна задается в виде квадратичной параболы так, чтобы пьезометрическая кривая по границе областей касалась горизонтальной линии, представляющей давление в невозмущенной области. Распределение давления уже не будет стационарным, а градиент давления по границе областей становится равным нулю, что обеспечивает плавное смыкание профиля давлений в возмущенной и невозмущенной областях.

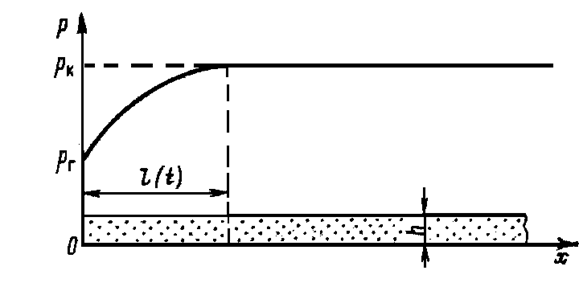Рис. 53

Рассмотрим прямолинейно-параллельный фильтрационный поток упругой жидкости (рис.53). В горизонтальном пласте постоянной толщины h и ширины B пущена в эксплуатацию галерея с постоянным дебитом Q . К моменту времени t после пуска граница возмущенной области продвигается на величину 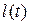, при этом кривая распределения давления в этой области задается в виде параболы так, что в точке 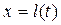касательная к параболе горизонтальна, т.е.

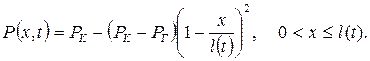(7.61)

Дебит галереи определяется по закону Дарси

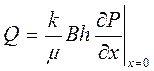. (7.62)

Учитывая (7.61), находим выражение для дебита галереи

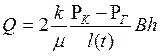. (7.63)

Закон движения внешней границы возмущенной области определяется из уравнения материального баланса (как и при методе ПССС) и имеет вид:

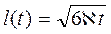. (7.64)

Распределение давления (7.61) в возмущенной области пласта с учетом (7.63) и (7.64) принимает вид

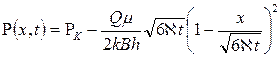, (7.65)

где ;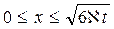

при .

Расчет депрессии 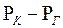по формуле (7.65) дает погрешность по сравнению с точным решением примерно 9%, т.е. в 2,5 раза меньше, чем метод ПССС.

Аналогичным образом строится решение и для случая плоскорадиального потока. В этом случае распределение давления в возмущенной области пласта задается в виде

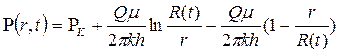, (7.66)

где R(t) - радиус внешней границы возмущенной области пласта.

Заметим, что отбросив последнее слагаемое в уравнении (7.66), получаем закон распределения давления при методе ПССС.