Метод последовательной смены стационарных состояний (ПССС)
Одним из наиболее простых по идее приближенных методов решения задач неустановившейся фильтрации является метод последовательной смены стационарных состояний (ПССС), развитый И.А. Чарным и широко применяемый в практических расчетах. Метод основан на предположении, что давление в пласте изменяется во времени значительно медленнее, чем по координатам. Поэтому в основном уравнении упругого режима фильтрации (7.10) производную по времени можно в первом приближении отбросить, в результате чего для давления получается уравнение Лапласа, описывающее стационарный процесс. В этом случае в каждый момент времени вся область движения жидкости, в действительности охватывающая весь пласт, условно разделяется на две области: возмущенную и невозмущенную. При этом предполагается, что в возмущенной области, начинающейся от стенки скважины, давление распространяется так, как будто бы движение жидкости в ней установившееся; внешняя граница этой области служит контуром питания.
В невозмущенной области пласта давление всюду постоянно и равно начальному статическому. Закон движения подвижной границы раздела возмущенной и невозмущенной областей определяется при помощи уравнения материального баланса и граничных условий.
Рассмотрим схематично применение метода ПССС для случаев плоскопараллельного и плоскорадиального потоков упругой жидкости.
Прямолинейно-параллельный фильтрационный поток.
Рассмотрим полубесконечный горизонтальный пласт во всей области которого первоначально существовало постоянное давление Рк. В начальный момент времени (t=0) в сечении Х=0 пласта толщиной h и шириной В давление внезапно снизилось и стало равным Рг= const. К некоторому моменту времени t>0 после пуска галереи граница возмущенной области распространилась на длину 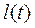 . (Рис.51) .
. (Рис.51) .
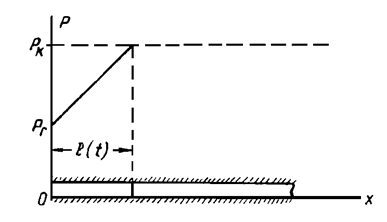
Рис.51
Распределение давления в возмущенной зоне принимается установившимся
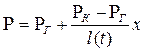 , (7.52)
, (7.52)
т.е. эпюра давлений Р(x) представляет собой прямую линию, перемещающуюся вдоль пласта с угловой точкой x= 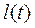 . Заметим, что в точном решении этой задачи эпюра давлений угловой точки не имеет.
. Заметим, что в точном решении этой задачи эпюра давлений угловой точки не имеет.
Рассматривая массу жидкости, отобранной за счет ее упругости из возмущенной области пласта 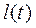 , ее массовый расход, выраженный по закону Дарси, получаем дифференциальное уравнение для границы
, ее массовый расход, выраженный по закону Дарси, получаем дифференциальное уравнение для границы 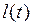 возмущенной зоны пласта, интегрирование которого дает закон движения этой границы:
возмущенной зоны пласта, интегрирование которого дает закон движения этой границы:
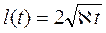 . (7.53)
. (7.53)
Тогда закон распределения давления в возмущенной зоне пласта (7.52) принимает вид
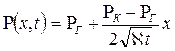 ,
,
или
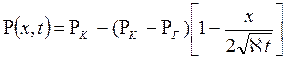 ; (7.54)
; (7.54)
где 0 < x £ 2 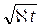 ;
;
а при x > 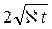 ,
, 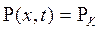 .
.
Нетрудно определить дебит галереи:
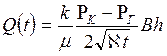 . (7.55)
. (7.55)
Погрешность расчета дебита галереи по приближенной формуле (7.55) по сравнению с расчетами по точной формуле (7.24) не превосходит 11%.
Плоскорадиальный фильтрационный поток.
Рассмотрим плоскорадиальный приток упругой жидкости к скважине радиуса rc из неограниченного горизонтального пласта постоянной толщины h (рис.52); скважина работает с постоянным дебитом Q; первоначально давление во всем пласте было одинаковым и равным Рк.
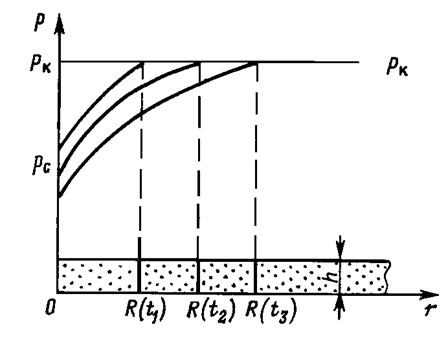
Рис. 52
После пуска скважины в работу вокруг нее образуется воронка депрессии, которая теоретически охватывает весь пласт. Приближение в решении задачи заключается в том, что мы последовательно во времени фиксируем радиус воронки депрессии, т.е. в каждый момент времени радиус воронки R(t) принимается как конечная величина. При этом кривая распределения давления аппроксимируется логарифмической кривой, т.е.

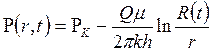 . (7.56)
. (7.56)
При этом дебит скважины будет описываться формулой, аналогичной формуле Дюпюи:
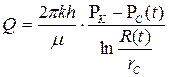 . (7.57)
. (7.57)
Размер возмущенной области R(t) также находится из рассмотрения уравнения материального баланса для упругой жидкости, отобранной из этой области пласта. В итоге закон движения границы R(t) возмущенной зоны пласта имеет вид:
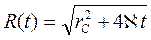 . (7.58)
. (7.58)
Тогда из равенства (7.56) находится давление в любой точке пласта в любой момент времени t:
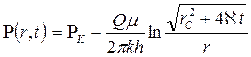 , (7.59)
, (7.59)
где 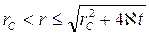 ,
,
а при 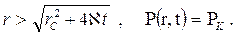
Депрессия на скважине (r = rC) в момент t будет:
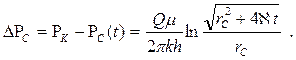 (7.60)
(7.60)
Сравнивая (7.60) с депрессией, определенной по точной формуле (7.39), убеждаемся, что относительная погрешность уменьшается с течением времени и составляет:
10,6 % , если 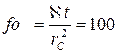 ;
;
7,5 %, если 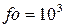 ;
;
5,7 %, если 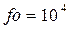 .
.
Дата добавления: 2016-11-04; просмотров: 4914;











