Нивелирование по квадратам

Нивелирование поверхности — один из способов топографической съемки, при котором на местности по определенному правилу располагают точки, высоты которых определяют геометрическим нивелированием. Наибольшее практическое применение имеет метод квадратов и метод магистралей с поперечными профилями. Создание плана по результатам нивелирования по квадратам начинают с разбивки в заданном масштабе сетки квадратов, у каждой выписывают округленную до сантиметра высоту. Согласно абрису наносят и вычерчивают в условных знаках ситуацию, а затем путем интерполирования горизонталями изображают рельеф.

Топографическую съемку небольших участков равнинной местности с небольшим количеством контуров при высоте сечения рельефа через 0,1; 0,25; 0,5 м выполняют нивелированием поверхности по квадратам, прямоугольникам, характерным линиям рельефа и т. п. Отметки пикетов во всех способа определяют точек.

При нивелировании по квадратам геометрическим нивелированием, различие состоит в методе определения планового положения и мерным прибором на местности разбивают сетку квадратов, в вершинах квадратов забивают колышки. Сначала строят квадраты со сторонами 100, 200 или 400 м, а затем получая более мелкие квадраты со сторонами 40 м при съемке в масштабе 1:2000, 20 м — при съемке в масштабе 1:1000 и 1:500. При разбивке квадратов выполняют съемку ситуации. Результаты съемки фиксируют в абрисе (рис. 1).

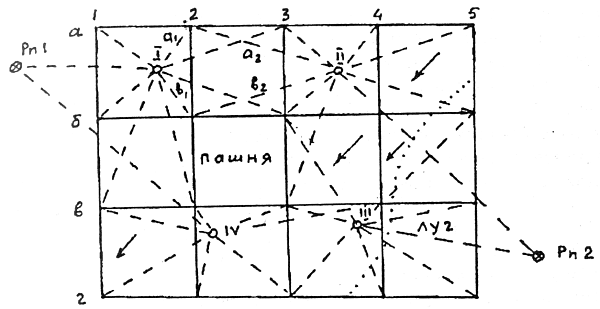
Рис. 1. Абрис нивелирования поверхности по квадратам (стрелками показано направление скатов).

Нивелир устанавливают так, чтобы с меньшего количества станций выполнить съемку всего участка. Установив нивелир на станции I, берут отсчет по рейке, поставленной на опорной высотной точке (например на Рп I) и вычисляют:

ГП = Нрn + а,

где Нрn — отметка репера; а — отсчет по рейке, установленной на репере. У номеров вершин квадратов выписывают отсчеты по рейкам, установленным на них, в абрисе штриховыми линиями показывают, на какие вершины квадратов выполнено нивелирование с данной станции. Отметки вершин квадратов вычисляют по формуле:

Нi = ГП - а

Подобным образом выполняют нивелирование и с других станций с обязательным определением ГП на каждой станции по опорным высотным пунктам или связующим точкам. С каждой последующей станции нивелируют несколько связующих точек, при этом (см. рис. 1.27) а1+ b2 = а2 + b1, расхождение между этими суммами не должно превышать 10 мм.

Тригонометрическое нивелирование - метод определения разностей высот точек на земной поверхности по измеренному углу наклона и длине наклонной линии визирования или её проекции на горизонтальную плоскость.

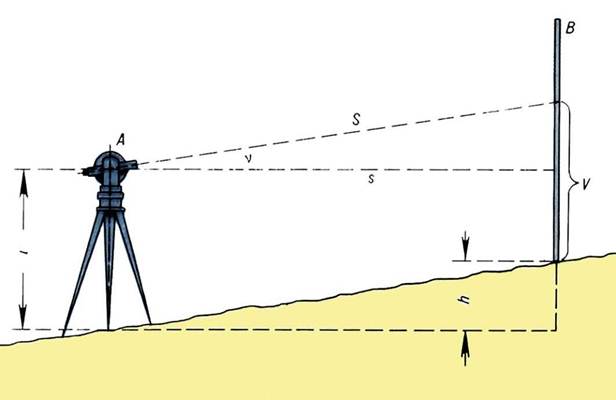
Рис.5 – Тригонометрическое нивелирование

Тригонометрическое нивелирование:

i - высота прибора;

V - высота визирования;

h - разность высот (превышение) между точками A и B;

S - линия визирования; s - горизонтальная проекция линии визирования;

n - угол наклона визирного луча.

Превышение h (рис.5) определяют по формулам:

h = s * tg ν + i - V или

h = S * sin ν + i - V,

где ν - угол наклона визирного луча;

S - длина линии визирования;

s - горизонтальная проекция;

i - высота прибора;

V - высота визирования.

Тригонометрическое нивелированиеприменяется при топогеодезических работах на земной поверхности и маркшейдерских съёмках в горных выработках, наклоны которых свыше 8°.

Тригонометрическое нивелирование называют также геодезическим или нивелированием наклонным лучом. Оно выполняется теодолитом; для определения превышения между двумя точками нужно измерить угол наклона и расстояние. В точке А устанавливают теодолит, в точке В - рейку или веху известной высоты V. Измеряют угол наклона зрительной трубы теодолита при наведении ее на верх вехи или рейки (рис.6 4.38). Длину отрезка LK можно представить как сумму отрезков LC и CK с одной стороны и как сумму отрезков LB и BK с другой. Отрезок LC найдем из ΔJLC: LC = S*tg ν , остальные отрезки обозначены на рисунке.

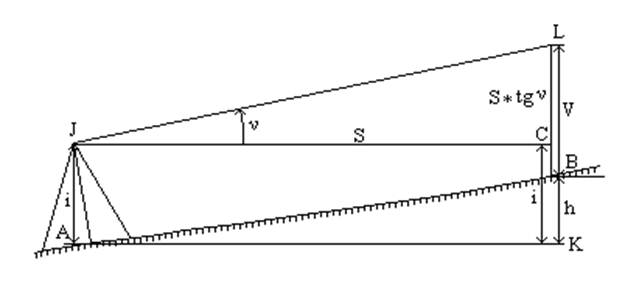
Рис.6 4.38 – Измерение угла наклона зрительной трубы теодолита

Тогда

LC + CK = LB + BK и S * tg( ν) + i = V + h.

Отсюда выразим превышение h

h = S * tg(ν) + i - V. (7 4.67)

Выведем формулу превышения из тригонометрического нивелирования с учетом кривизны Земли и рефракции. Вследствие рефракции луч от верхнего конца вехи идет по кривой, а визирная линия трубы будет направлена по касательной к этой кривой в точке J. Визирная линия трубы пересечет продолжение вехи в точке L1, а не L. Проведем уровенные поверхности в точках A, B, J (рис.7 4.39).

Проведем касательную к уровенной поверхности в точке J и обозначим: высоту прибора - i, высоту вехи - V, горизонтальное проложение линии AB - S.

Превышение точки B относительно A выражается отрезком BK. Отрезок L1K на рис. 7 4.39 - Тригонометрическое нивелирование с учетом кривизны Земли и рефракции можно выразить через его части двумя путями:

L1K = L1E + EF + FK,

L1K = L1L + LB + BK.

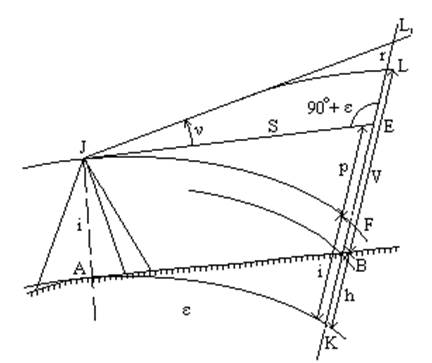
Рис. 7 4.39 - Тригонометрическое нивелирование с учетом кривизны Земли и рефракции

Отрезок L1E найдем из Δ JL1E. Этот треугольник можно считать прямоугольным, так как угол L1EJ очень мало отличается от прямого, всего лишь на величину центрального угла ε =(S / R)*r. Этот угол при S = 1 км не превосходит 0.5'.

Итак,

L1E = JE * tg(ν),

но поскольку JE = S, то L1E = S * tg(ν).

Отрезок EF выражает влияние кривизны Земли:

EF = p = S2 / 2*R;

отрезок FK равен высоте прибора FK = i; отрезок L1L выражает влияние рефракции:

L1L = r * (S2 / 2*R) * k = p * k;

отрезок LB равен высоте вехи V.

Таким образом,

S * tg(ν) + p + i = r + V + h,

откуда

h = S * tg(ν) + (i - V) + (p - r),

или

h = S * tg(ν) + (i - V) + f. (8 4.68)

При измерении расстояния с помощью нитяного дальномера формула превышения несколько изменяется; так как S = (Cl + c)* Cos2(ν), то

h = 0.5*(Cl + c)*Sin(2*ν) + i - V + f = h'+ i - V + f,

Величину h'= 0.5*(Cl + c)*Sin(2*ν) называют тахеометрическим превышением.

При S = 100 м величиной f можно пренебречь, так как f = 0.66 мм .

S2 , где S - расстояние (в сотнях метров).

Ошибка измерения превышения из тригонометрического нивелирования оценивается величиной от 2 см до 10 см на 100 м расстояния.

При последовательном измерении превышений получается высотный ход; в высотном ходе углы наклона измеряют дважды: в прямом и обратном направлениях.