Библиографический список

6.1. Евсеев, Д. Г. Физические основы процесса шлифования / Д. Г. Евсеев, А. Н. Сальников. – Саратов : Изд-во Сарат. ун-та, 1978. – 128 с.

6.2. Унянин, А. Н. Повышение эффективности совмещенного шлифования путем рационального применения технологических жидкостей: Дис. … канд. техн. наук: 05.02.08 / Ульян. политехн. ин-т. – Ульяновск, 1986. – 229 с.

6.3. Худобин, Л. В. Минимизация засаливания шлифовальных кругов / Л. В. Худобин, А. Н. Унянин. – Ульяновск : УлГТУ, 2007. – 298 с.

6.4. Марочник сталей и сплавов / А. С. Зубченко, М. М. Колосков, Ю. В. Каширский [и др.]; под общ. ред. А. С. Зубченко. – 2-е изд., доп. и испр. – М. : Машиностроение, 2003. – 784 с.

6.5. Чередниченко, Г. И. Физико-химические и теплофизические свойства смазочных материалов / Г. И. Чередниченко, Г. Б. Фройштетер, М. П. Ступак. – Л. : Химия, 1986. – 224 с.

Моделирование локальных температур при шлифовании

При теплофизическом анализе процесса шлифования различают средние контактные и локальные температуры. Влияние средних контактных температур на показатели процесса шлифования рассмотрено в подразделе 6.2.

Локальными называют температуры на поверхностях контакта абразивного зерна (АЗ) со стружкой и заготовкой. Эти температуры влияют на интенсивность истирания, адгезионного, диффузионного изнашивания и окисления АЗ и налипания на них материала обрабатываемой заготовки [7.1 – 7.4]. Локальные температуры оказывают влияние на структурно-фазовые превращения в поверхностном слое обработанной детали. Определяя интенсивность напряжений, возникающих при деформировании материала заготовки, локальные температуры влияют на силовую напряженность процесса шлифования, а следовательно, и на его производительность [7.5].

Таким образом, без расчета локальных температур невозможно оценить работоспособность шлифовального круга (ШК), производительность шлифования и качественные характеристики шлифованных деталей.

Определение локальных температур путем натурных экспериментов затруднительно, поэтому для этих целей широко используют моделирование.

Для расчета этих температур разработаны физические и математические модели, позволяющие в комплексе учесть расположение отдельных источников тепловыделения относительно контактирующих при шлифовании объектов (АЗ, заготовки и стружки), наложение тепловых импульсов от отдельных зерен, зависимость теплофизических свойств контактирующих объектов и механических свойств материала заготовки от температуры, а также условия охлаждения этих объектов [7.1].

При схематизации объектов, участвующих в теплообмене, АЗ представлено в настоящей лабораторной работе в виде усеченной пирамиды с углом при вершине 2γ и площадкой затупления размерами l₂, отдающей в массу круга часть теплоты. Форма заготовки принята в виде прямоугольного параллелепипеда; стружка, имеющая переменную толщину, представлена в виде совокупности прямоугольных параллелепипедов различной толщины. Пограничные слои между АЗ, стружкой и заготовкой и их термическое сопротивление не учитываются, так как контакт между этими телами в условиях пластической деформации приближается к идеальному. Поэтому можно считать, что температура поверхностей контактирующих тел в любой точке их соприкосновения одна и та же.

Теплообмен является нестационарным, поскольку АЗ вступают в контакт с заготовкой периодически. Принимаются во внимание источники тепловыделения в зоне деформирования и в зонах контакта АЗ со стружкой и заготовкой. Вследствие изменения глубины внедрения АЗ в материал заготовки по длине контакта плотности тепловых потоков, эквивалентные работе деформирования и трению стружки об АЗ, непостоянны при его перемещении. Для повышения достоверности результатов расчетов учтена зависимость сопротивления материала заготовки деформированию и зависимость теплофизических свойств всех взаимодействующих объектов от температуры.

Общая мощность тепловыделения при работе режущего АЗ

W_i = W_D + W_1T + W_2T ,

где W_D, W_1T и W_2T – мощность тепловыделения источников, возникающих как результат перехода в теплоту работы соответственно деформирования (W_D) и работы сил трения стружки о зерно (W_1T) и зерна о заготовку (W_2T), Вт.

Все источники тепловыделения считаются двумерными, что не вносит существенных погрешностей в результаты расчета [7.2]. Мощности источников:

W_1T = P₁ · V₁;

W_2T = P_{z тр} · V_к;

W_D = (P_zi – P_{z тр}) · V_к – Р₁ · V₁,

где P_zi – касательная составляющая силы диспергирования единичным зерном, Н; Р₁ и P_{z тр} – силы трения соответственно между стружкой и зерном и между зерном и заготовкой, Н; V_к – рабочая скорость круга, м/с; V₁ = V_к / η – скорость перемещения стружки относительно АЗ, м/с; η – коэффициент усадки стружки.

Принимая во внимание известные зависимости для расчета сил диспергирования и трения при работе единичного зерна [7.2 – 7.5], для расчета мощностей тепловыделения получены следующие выражения:

;

,

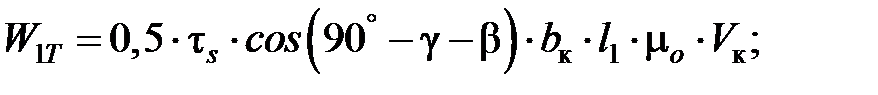
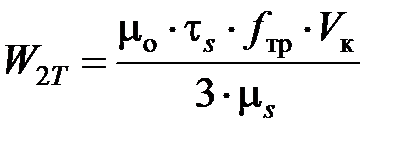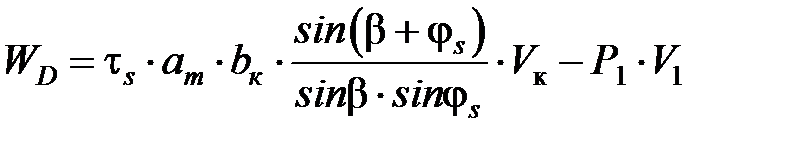где 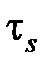– напряжение сдвига, Па; a_m – глубина внедрения зерна в заготовку, м; b_к – ширина среза, м; 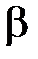– угол сдвига, град.; 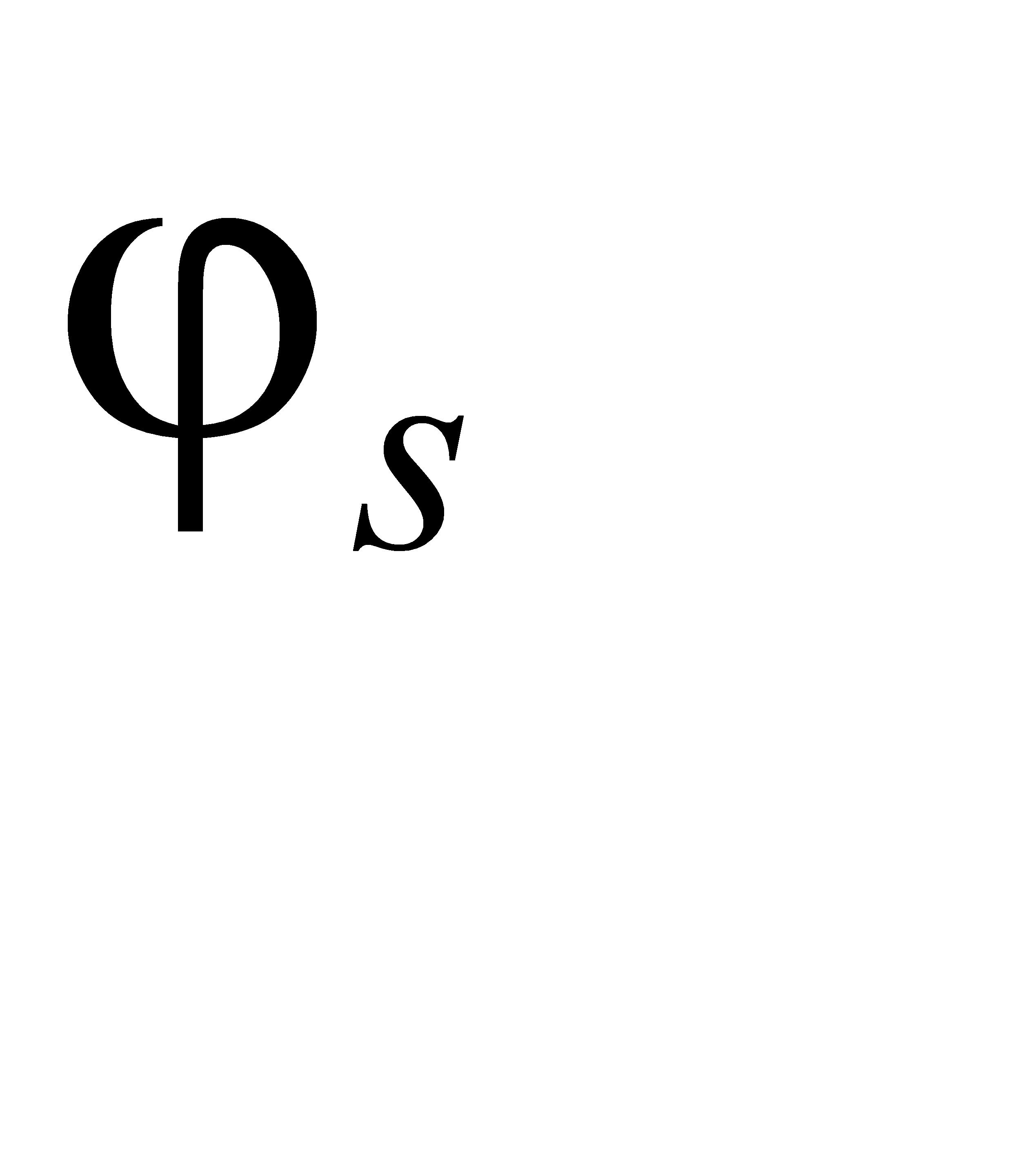– угол внутреннего трения, град.; μ_s – коэффициент внутреннего трения в плоскости сдвига; 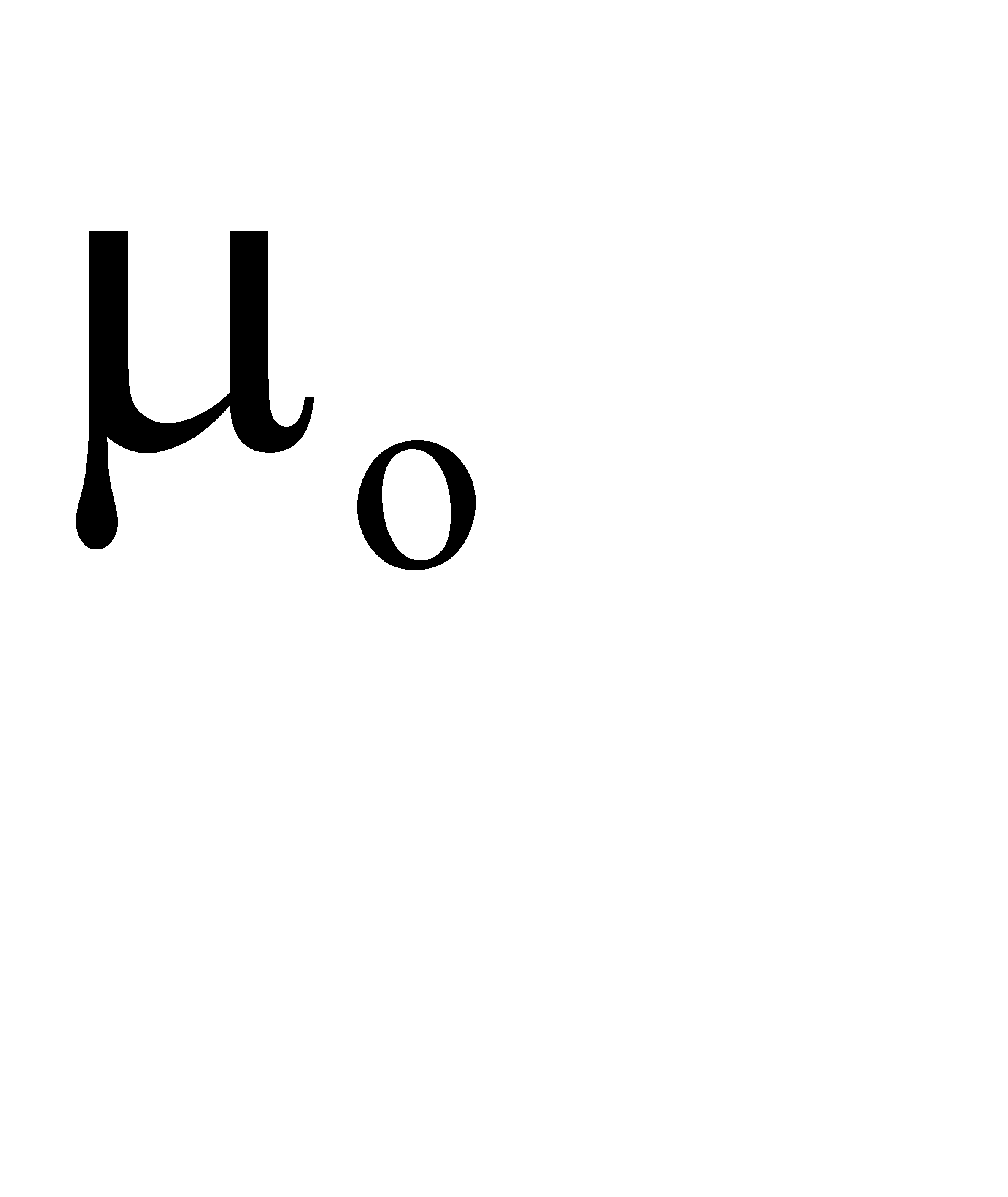– коэффициент внешнего трения; f_тр – площадь поверхности трения зерна о заготовку, м²; l₁ – длина контакта стружки с поверхностью АЗ, м; γ – угол при вершине АЗ, град.

Учтено, что средние по плоскости сдвига касательные напряжения связаны с интенсивностью напряжений при скорости и температуре деформации процесса шлифования σ_iш зависимостью 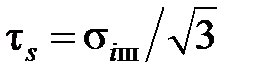[7.5].

На схеме теплообмена, показанной на рис. 7.1, действительная траектория движения режущего зерна представлена в виде прямой линии FB₁.

Считается, что источник плотностью q_D, возникающий на плоскости сдвига, распределен равномерно, а соответствующая плотность тепловыделения

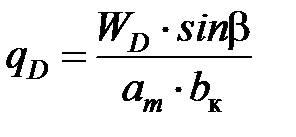. (7.1)

Плотность тепловыделения источника, действующего на поверхности контакта стружки с АЗ, принята распределенной по несимметричному нормальному закону с максимальной плотностью потока

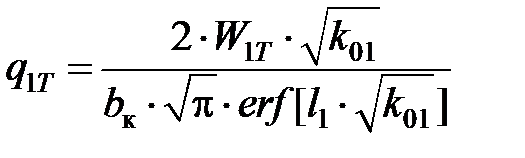, (7.2)

где k₀₁ – коэффициент, м^-2; erf – функция, называемая интегралом вероятности.

Плотность тепловыделения в точке, расположенной на расстоянии х_u от точки с максимальной плотностью тепловыделения,

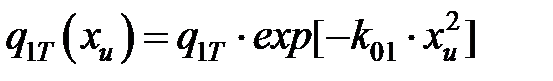. (7.3)

Плотность тепловыделения на участке контакта АЗ с заготовкой принята распределенной по экспоненциальному закону (аналогично закону распределения нормальных напряжений), а максимальная плотность тепловыделения

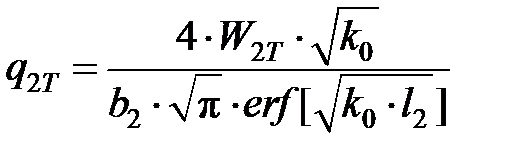; (7.4)

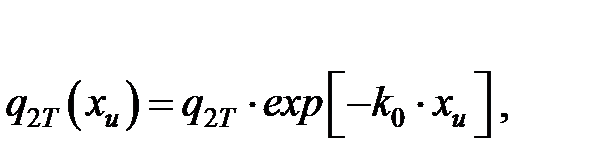(7.5)

где k₀ – коэффициент, м^-2 ; l₂ – размер площадки затупления на АЗ, м.

Считается, что заготовка 1 неподвижна, а режущее зерно 2, ШК 4, стружка 3 и плоскость сдвига DE перемещаются относительно заготовки со скоростью, равной сумме скорости V_к и скорости подачи V_sпр (см. рис. 7.1). Система координат xоy связана с зерном и учтено, что она перемещается относительно заготовки в направлении оси ox со скоростью V_к.

Уравнения теплопроводности для заготовки 1, режущего зерна 2, стружки 3 и ШК 4 имеют следующий вид:

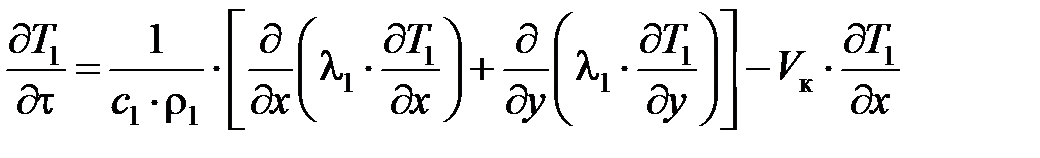; (7.6)

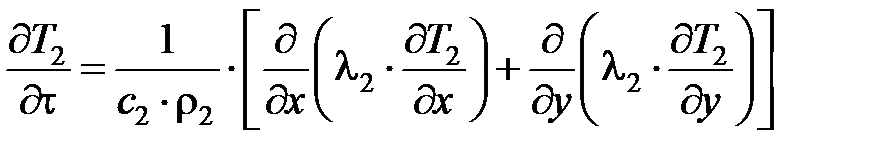; (7.7)

у

l2

γ

Q

P

Vк

q1т

М N

D

C

am

А

β

Е

q¶

q2т

lк

V

F

G

x

H

W

K

L

S

В

В1

Рис. 7.1. Схема теплообмена в зоне контакта режущего АЗ с заготовкой: 1 – заготовка; 2 – АЗ; 3 – стружка; 4 – ШК

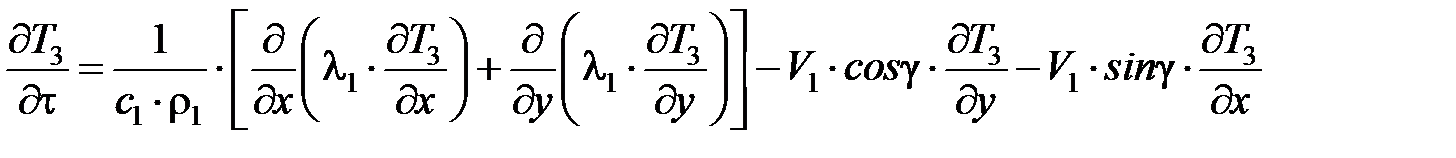; (7.8)

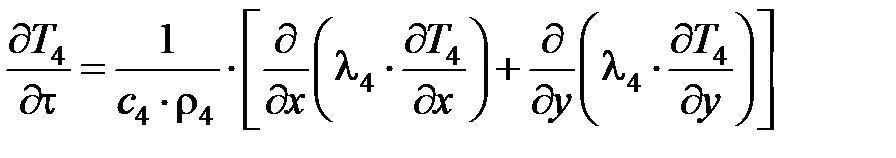, (7.9)

где λ₁, λ₂, λ₄ – коэффициенты теплопроводности, Вт/(м·К); с₁, с₂, с₄ – теплоемкости, Дж/(кг · К); ρ₁, ρ₂, ρ₄, – плотности, кг / м³; Т₁, Т₂, Т₃, Т₄ – температуры контактирующих объектов, К. (Индексы 1 – 4 относятся к заготовке, зерну, стружке и ШК соответственно.)

Начальное условие

Т(x, y, О) = Т_о

означает равенство в начальный момент времени температур любой точки контактирующих объектов температуре окружающей среды.

Условия взаимодействия поверхностей обрабатываемой заготовки, зерна, стружки, ШК и окружающей среды описываются следующими граничными условиями:

– в пределах зоны контакта заготовки 1 с зерном 2 (см. рис. 7.1):

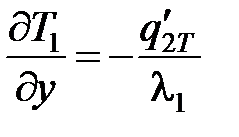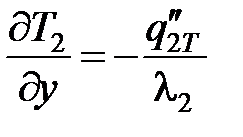; ; Т₁ = Т₂; ;

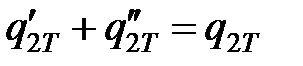– в пределах зоны контакта заготовки 1 со стружкой 3:

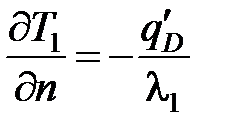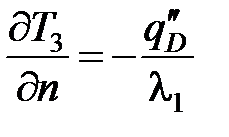; ; Т₁ = Т₃; ,

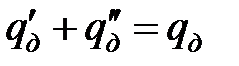– в пределах зоны контакта стружки 3 с АЗ 2:

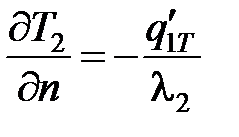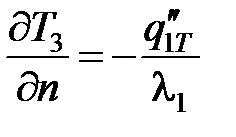; ; Т₂ = Т₃; .

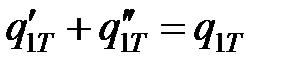Сопряжение АЗ со связкой круга является идеальным, а это означает равенство температур сопряженных поверхностей зерна 2 и круга 4, т. е. Т₂ = Т₄ .

Теплообмен на границах объектов, контактирующих с СОЖ или воздухом, задан в форме закона Ньютона-Рихмана, описывающего процесс конвективного теплообмена, в виде

,

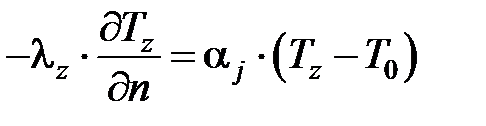где z – номер объекта (z = 1, 2, 3, 4 для заготовки, АЗ, стружки и круга соответственно); j – номер поверхности; α_j – коэффициент теплоотдачи от j-й поверхности, Вт/(м²∙К).

Границы PQ и WS области PQWS шлифовального круга считаются теплоизолированными.

Время, в течение которого происходит теплообмен, разбито на конечные малые промежутки Δτ. Число положений АЗ относительно дуги контакта с заготовкой

,

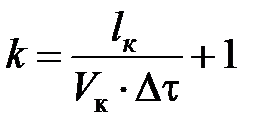где l_к – длина контакта ШК с заготовкой, м.

Глубина внедрения АЗ в заготовку при его i-м положении

a_mi = a_кр + а_зi,

где a_кр – критическая глубина микрорезания, м; а_зi – подача на АЗ при i-м положении последнего:

,

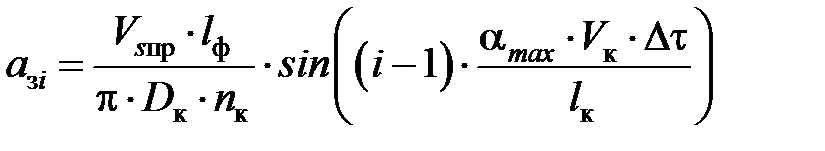где l_ф – среднее расстояние между диспергирующими зернами, м; n_к – частота вращения ШК, с^-1; V_sпр– скорость продольной подачи, м/с; D_к – диаметр наружной поверхности ШК, м; α_max – угол, град., определяемый как

α_max = arc cos ,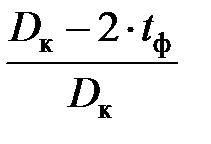

где t_ф – глубина шлифования, м.

На каждый элементарный участок заготовки от момента входа его в зону действия тепловых импульсов до момента выхода из этой зоны воздействует ряд импульсов, являющихся результатом диспергирования материала заготовки отдельными АЗ. Для расчета количества тепловых импульсов, воздействующих на каждый элементарный участок, используется зависимость

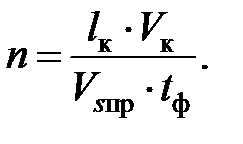
Чтобы учесть взаимное влияние тепловых импульсов, необходимо моделировать движение по траектории FB₁ (см. рис. 7.1) зерен, число которых равно n. Начальная температура заготовки при воздействии на нее j-го АЗ (2 ≤ j ≤ n) принята равной температуре, до которой она успевает остыть после прохождения (j – 1)-го зерна. При моделировании температурного поля от первого зерна начальная температура принята равной температуре окружающей среды.

Невозможность априорного определения плотностей распределения тепловых потоков между контактирующими объектами, изменение положения зон тепловыделения во времени, необходимость учета зависимости теплофизических свойств контактирующих объектов и механических свойств материала заготовки от температуры создают серьезные трудности для аналитического определения локальных температур. Однако эту задачу можно решить численным методом, используя метод конечных элементов [7.6].

При построении дискретных аналогов дифференциальных уравнений теплопроводности используют универсальный метод баланса. Для каждого типа расчетных элементов зерна, заготовки, стружки и ШК методом баланса получены дискретные аналоги соответствующих дифференциальных уравнений теплопроводности (7.6) – (7.9). Каждому расчетному элементу присвоен уникальный двухкомпонентный номер i, j, в котором i – номер расчетной точки в направлении оси 0x (рис. 7.2); j – то же в направлении оси 0y.

Из закона сохранения энергии следует, что сумма всех входящих и выходящих за время Δτ тепловых потоков (см. рис. 7.2) равна изменению энтальпии рассматриваемого элемента (конечного объема):

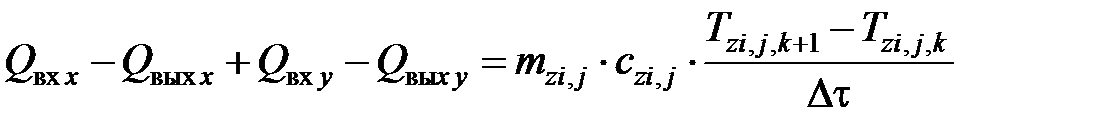, (7.10)

где Q_{вх х}, Q_{вых х} – тепловой поток, соответственно входящий в элемент (i, j) и выходящий из него в направлении оси 0х, Вт; Q_{вх у}, Q_{вых у} – то же в направлении оси 0у; 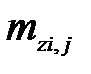– масса расчетного элемента, кг; 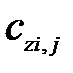– удельная теплоемкость объекта, Дж/(кг · К); 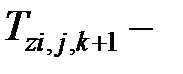температура расчетного элемента объекта в рассматриваемый момент времени, К; 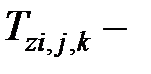то же в предыдущий момент времени, К; z – номер рассматриваемого объекта (z = 1, 2, 3, 4 соответственно для заготовки, зерна, стружки и ШК); подстрочный индекс, содержащий двухкомпонентный номер расчетного элемента, обозначает принадлежность соответствующего параметра к этому расчетному элементу.

Составляющие теплового баланса определяются следующими зависимостями:

; ; ; ,

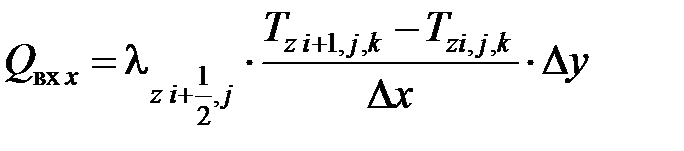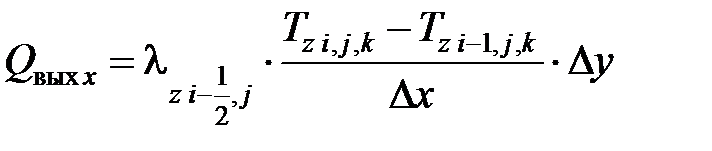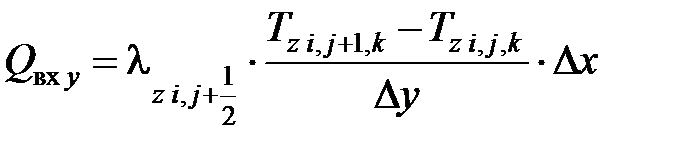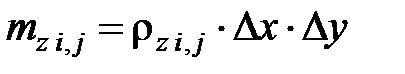где λ_z – теплопроводность z-го объекта, Вт/(м·К); Δх, Δу – расстояние между расчетными точками в направлении оси 0х и 0у соответственно, м.

Qвых у

(i, j – 1)

(i, j)

(i – 1, j)

Qвых х

Qвх х

(i + 1, j)

Qвх y

(i, j + 1)

Рис. 7.2. Баланс тепла типового расчетного элемента: – расчетные точки, задействованные в тепловом балансе; Qвх х, Qвых х – тепловой поток, соответственно входящий в элемент (i, j) и выходящий из него в направлении оси 0х; Qвх у, Qвых у – то же в направлении оси 0у

Дискретный аналог уравнения теплопроводности z-го объекта для типового расчетного элемента с внутренней расчетной точкой:

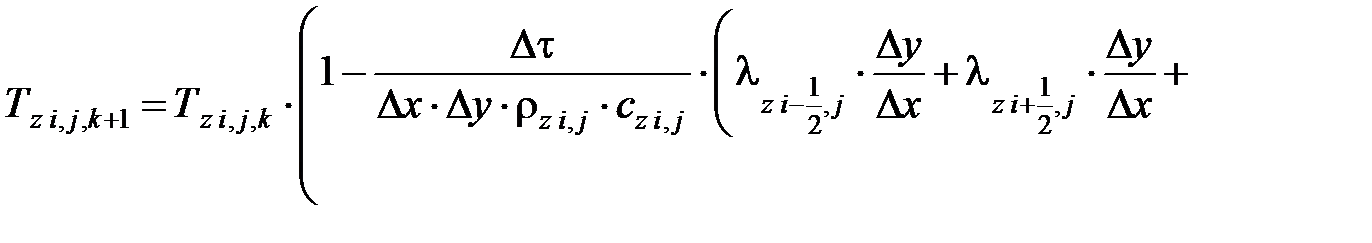
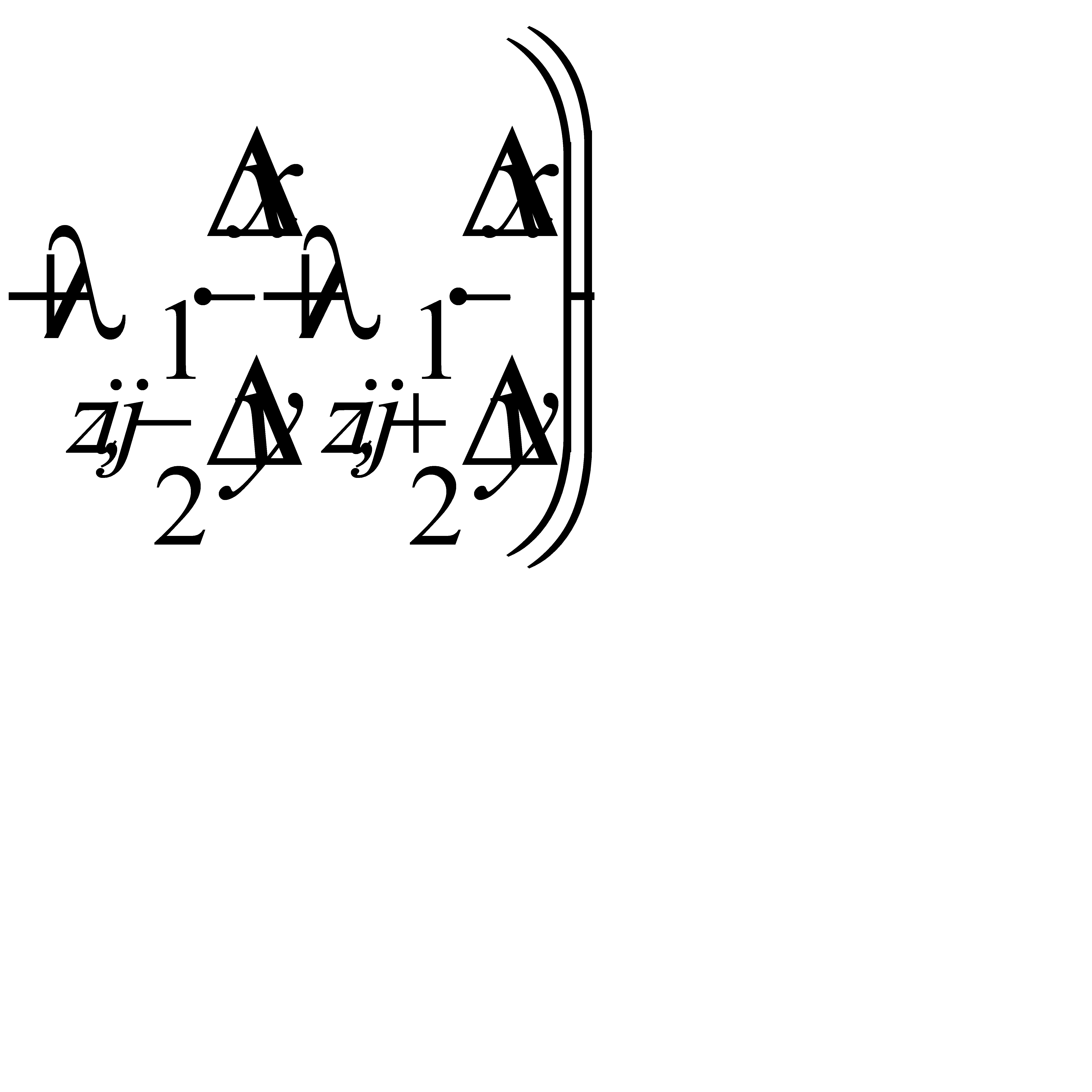
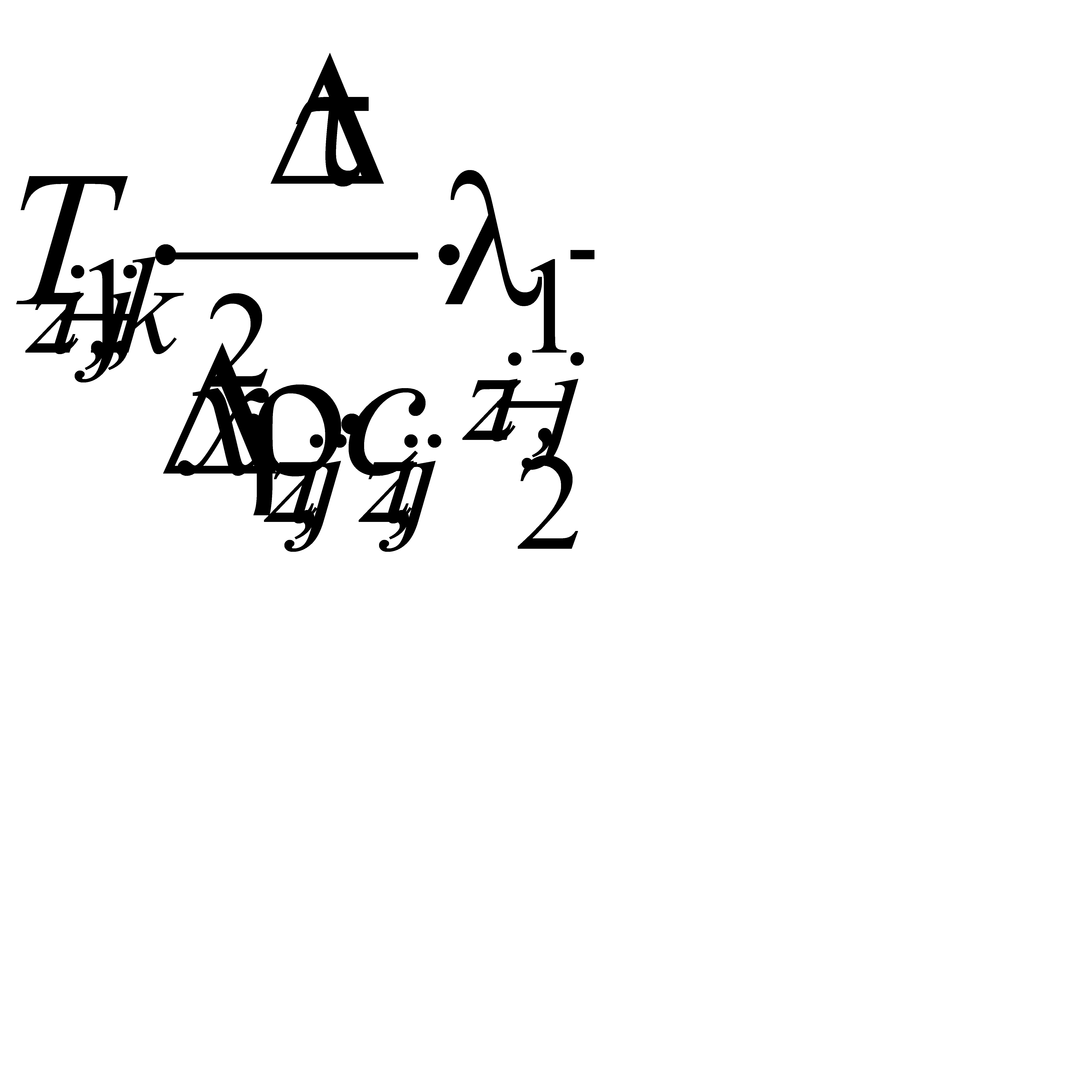
(7.11)

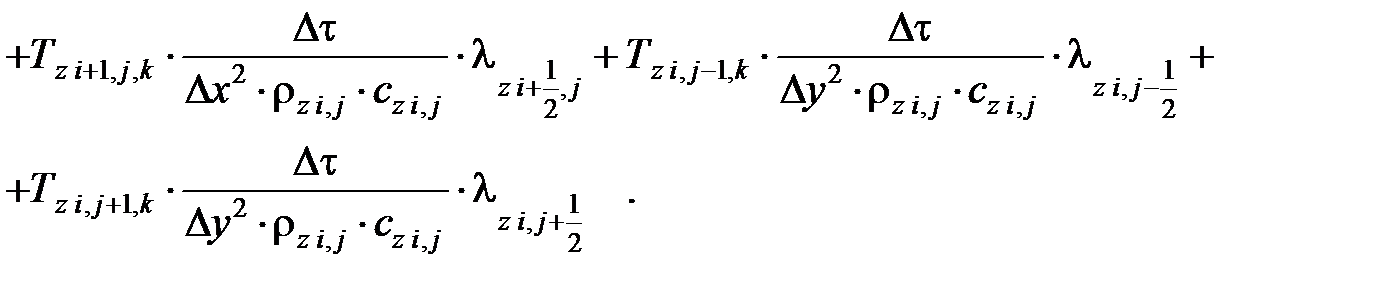
Дискретные аналоги дифференциальных уравнений теплопроводности для остальных расчетных элементов зон контакта объектов и на их поверхностях получены аналогично.

Методика численного расчета дискретных аналогов уравнений теплопроводности реализована в оригинальных программах для персонального компьютера на языке Microsoft Visual Basic. Перед началом расчета программа запрашивает исходные данные: размеры контактирующих объектов, материалы заготовки и АЗ, характеристику ШК, элементы режима шлифования, параметры техники подачи СОЖ, параметры расчетной сетки и др. После ввода исходной информации программа вычисляет устойчивый шаг интегрирования по времени и предлагает начать расчет. В результате работы программы рассчитывают температуры в расчетных точках контактирующих объектов (рис. 7.3).