Сифонный трубопровод
Сифонный трубопровод (сифон) представляет собой короткий трубопровод, соединяющий питающий резервуар А и приемный резервуар В, часть которого располагается выше уровня жидкости в резервуаре А (рис. 5.5). Разность уровней жидкости в резервуарах равна Н.
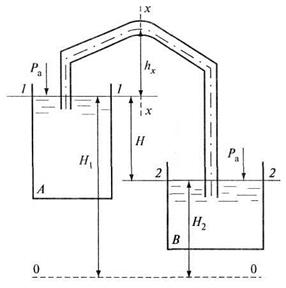
Рис. 5.5. Сифон
При возникновении в верхней части трубопровода давления меньше атмосферного создается разность давлений между атмосферным на поверхности жидкости питающего резервуара и вакуумметрическим давлением в верхней части сифона. За счет разности давлений при полном заполнении трубопровода сифона жидкость поднимается на высоту 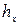 над уровнем в резервуаре А, а затем перетекает в приемный резервуар В.
над уровнем в резервуаре А, а затем перетекает в приемный резервуар В.
Для заполнения трубопровода жидкостью и создания вакуумметрического давления в верхней части сифона применяются вакуумные насосы.
Гидравлический расчет сифонных трубопроводов принципиально не отличается от расчета обычных водоводов.
Рассмотрим установившееся движение жидкости в сифонном трубопроводе. Напишем уравнение Бернулли для сечений 1-1 и 2-2, совпадающих с уровнями жидкости в резервуарах А и В, относительно плоскости сравнения 0-0 (см. рис. 5.5):
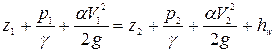 . (5.14)
. (5.14)
Давления в сечениях 1-1 и 2-2 соответствуют атмосферному 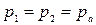 . Принимаем, что скорости в сечениях
. Принимаем, что скорости в сечениях 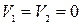 и
и 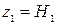 ;
; 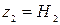 ,
, 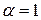 .
.
Из уравнения Бернулли получаем
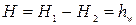 . (5.15)
. (5.15)
Гидравлические потери в трубопроводе
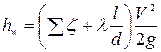 ,
,
где V - средняя скорость движения жидкости в трубе сифона; 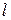 , d - длина и диаметр трубы сифона;
, d - длина и диаметр трубы сифона; 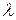 - коэффициент гидравлического трения;
- коэффициент гидравлического трения; 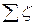 - сумма коэффициентов местных сопротивлений.
- сумма коэффициентов местных сопротивлений.
Расход жидкости через сифон согласно формуле (5.1) будет
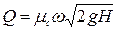 ,
,
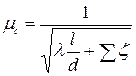 .
.
Для определения давления в верхнем сечении сифонного трубопровода (сечение х-х) составляем уравнение Бернулли для сечений 1-1 и х-х, в котором потери напора определяются на расстоянии 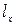 между этими сечениями.
между этими сечениями.
Плоскость сравнения в этом случае совпадает с плоскостью свободной поверхности в резервуаре А (сечение 1-1),  ,
, 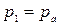 .
.
Давление в сечении х-х примем равным абсолютному 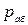 ,
, 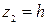 .
.
Подставляя в уравнение Бернулли известные величины, получаем
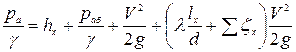 . (5.16)
. (5.16)
 Вакуумметрическое давление в верхнем сечении сифона х-х
Вакуумметрическое давление в верхнем сечении сифона х-х
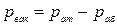 .
.
Из (5.16) вакуумметрический напор в верхнем сечении, 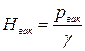 , равен
, равен
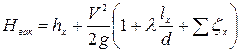 , (5.17)
, (5.17)
где 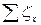 - суммарный коэффициент местных сопротивлений на участке трубопровода до сечения х-х.
- суммарный коэффициент местных сопротивлений на участке трубопровода до сечения х-х.
При расчете сифонов важным условием является определение давления в сечении трубопровода, наиболее высоко расположенного, где имеет место наибольшее разряжение. Для уменьшения разряжения в указанном сечении, возможно, окажется целесообразным увеличение сопротивления в нисходящей ветви сифона, что может быть осуществлено установкой задвижки за этим сечением. При этом нужно иметь в виду, что введение задвижки одновременно вызовет некоторое снижение расхода.
В результате уменьшения абсолютного давления в верхней части трубопровода может возникнуть кавитация. Кавитация произойдет, если давление насыщенных паров ( 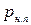 ) в трубопроводе будет больше абсолютного давления
) в трубопроводе будет больше абсолютного давления 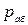 . При кавитации из жидкости будет выделяться растворимый газ и пузырьки пара, что приведет к снижению расхода жидкости в сифоне, и он может резко уменьшиться. Резкое снижение расхода в результате нарушения сплошности потока жидкости приводит к срыву работы сифона, подача жидкости в приемный резервуар В прекращается.
. При кавитации из жидкости будет выделяться растворимый газ и пузырьки пара, что приведет к снижению расхода жидкости в сифоне, и он может резко уменьшиться. Резкое снижение расхода в результате нарушения сплошности потока жидкости приводит к срыву работы сифона, подача жидкости в приемный резервуар В прекращается.
В сифонных трубопроводах появление кавитации обусловливается геометрической конфигурацией и принципом действия самого сифона, верхней своей частью находящегося под давлением меньше атмосферного.
Для нормальной работы сифонного трубопровода необходимо, чтобы минимальное абсолютное давление в верхней его части было больше давления насыщенных паров 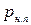 :
:
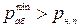 ,
, 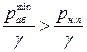
Давление 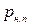 увеличивается с повышением температуры жидкости.
увеличивается с повышением температуры жидкости.
Таблица 5.2
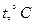
| ||||||||||
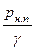 , м , м
| 0,12 | 0,24 | 0,43 | 0,75 | 1,25 | 2,00 | 3,17 | 4,82 | 7,14 | 10,3 |
В табл. 5.2 приведены значения 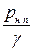 в метрах водяного столба в зависимости от температуры
в метрах водяного столба в зависимости от температуры 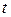 .
.
♦ Пример 5.2
Из источника водоснабжения вода подается в напорный резервуар (см. рис. 5.4). Расход воды 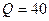 л/с. Высота оси насосной установки над уровнем воды в водоеме
л/с. Высота оси насосной установки над уровнем воды в водоеме 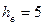 м. Высота подъема воды в напорный резервуар
м. Высота подъема воды в напорный резервуар 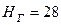 м. Длина всасывающей трубы
м. Длина всасывающей трубы 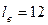 м. Длина магистральной напорной трубы
м. Длина магистральной напорной трубы 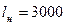 м. Коэффициент гидравлического трения
м. Коэффициент гидравлического трения 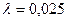 . Суммарный коэффициент местных сопротивлений во всасывающей трубе
. Суммарный коэффициент местных сопротивлений во всасывающей трубе 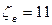 . Трубы чугунные. В напорном водоводе
. Трубы чугунные. В напорном водоводе 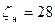 . Определить диаметры всасывающей и напорной труб, а также потребный напор.
. Определить диаметры всасывающей и напорной труб, а также потребный напор.
Диаметр всасывающей трубы определим, полагая 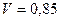 м/с:
м/с:
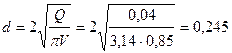 м.
м.
Принимаем диаметр  мм. Средняя скорость во всасывающей трубе
мм. Средняя скорость во всасывающей трубе
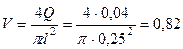 м/с.
м/с.
Гидравлические потери напора во всасывающей трубе
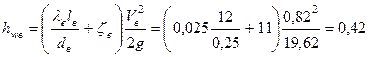 м.
м.
Вакуумметрический напор на входе в насос
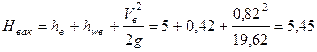 м.
м.
Зная кавитационную характеристику лопастного насоса 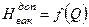 , необходимо сопоставить значения вычисленного
, необходимо сопоставить значения вычисленного 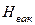 и допустимого вакуумметрического напора насоса
и допустимого вакуумметрического напора насоса 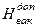 . В случае
. В случае 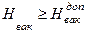 насос будет работать в кавитационном режиме. Например,
насос будет работать в кавитационном режиме. Например, 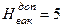 м при расходе
м при расходе 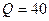 л/с. В этом случае необходимо установить насос ниже относительно уровня воды в водоеме, т.е.
л/с. В этом случае необходимо установить насос ниже относительно уровня воды в водоеме, т.е. 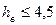 м.
м.
Диаметр напорной трубы принимаем таким же, как и всасывающей: 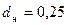 м.
м.
Гидравлические потери в напорной линии

Потребный напор
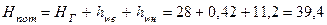 м.
м.
Зная расход 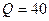 л/с и потребный напор
л/с и потребный напор 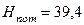 м, можно по каталогу насосов подобрать определенный тип насоса.
м, можно по каталогу насосов подобрать определенный тип насоса.
♦ Пример 5.3
Какое избыточное давление 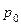 необходимо поддерживать в закрытом резервуаре с водой, чтобы через вентиль на конце трубопровода проходил расход
необходимо поддерживать в закрытом резервуаре с водой, чтобы через вентиль на конце трубопровода проходил расход 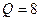 м3/ч. Вентиль располагается на высоте
м3/ч. Вентиль располагается на высоте 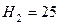 м, при некотором закрытии вентиля принять
м, при некотором закрытии вентиля принять 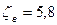 . Трубопровод состоит из труб длиной
. Трубопровод состоит из труб длиной  м,
м, 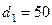 мм и
мм и 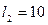 м,
м, 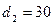 мм. Эквивалентную шероховатость принять
мм. Эквивалентную шероховатость принять 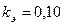 мм. Уровень воды (
мм. Уровень воды ( 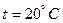 ) в резервуаре составляет
) в резервуаре составляет 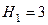 м (рис. 5.6).
м (рис. 5.6).
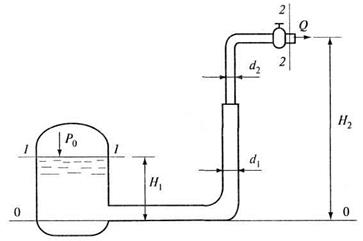
Рис. 5.6. К примеру 5.3
Составляем уравнение Бернулли, приняв первое сечение 1-1 по свободной поверхности воды в закрытом резервуаре, второе сечение 2-2 - за вентилем на конце трубопровода. Плоскость сравнения - горизонтальная, проходящая по оси начального участка трубопровода (см. рис. 5.6):
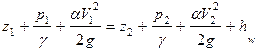 ;
;
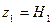 ;
;  ;
; 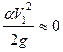 ;
; 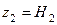 ;
; 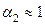 ;
; 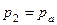 ;
;
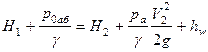 ,
,
где 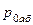 - абсолютное давление;
- абсолютное давление; 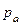 - относительное давление.
- относительное давление.
Таким образом,
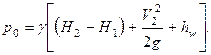
Потери напора
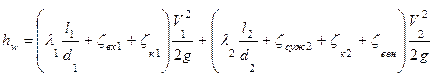 .
.
Полагаем, что потери по длине соответствуют координатной области сопротивления.
Вычисляем 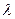 по формуле Шифринсона (4.104):
по формуле Шифринсона (4.104):
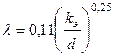 ;
;
 ;
;
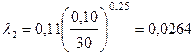 .
.
Коэффициент местного сопротивления на входе в трубу 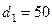 ;
; 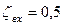 , колена
, колена  (табл. П1.4 приложения).
(табл. П1.4 приложения).
При внезапном сужении трубопровода коэффициент сопротивления вычисляется по формуле И. Идельчика (4.144):
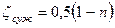 ,
,
где 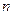 - показатель сужения потока.
- показатель сужения потока.
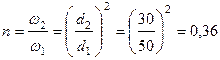 ;
;
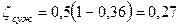 .
.
Расход 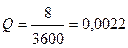 м3/с.
м3/с.
Средние скорости на участках трубопровода:
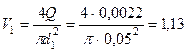 м/с;
м/с;
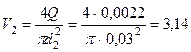 м/с.
м/с.
Коэффициенты системы первого и второго трубопроводов
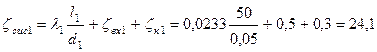 ;
;
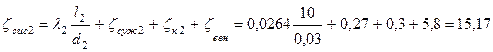 .
.
Потери напора
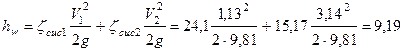 м.
м.
Избыточное давление (принимаем 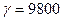 Н/м3)
Н/м3)
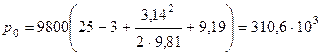 Па
Па 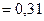 МПа.
МПа.
Дата добавления: 2016-10-26; просмотров: 10982;











