Таблицы принятия решений
Таблица принятия решений (таблица решений) является табличной формой представления множества продукционных правил. Таблицы решений применяются с 60-х годов в различных областях, например, в задачах автоматизации проектирования технологических процессов.
Идея таблиц решений заключается в использовании их в качестве декларативного представления алгоритмов в постановках задач и одновременно в качестве средства программирования на исходном языке, т.е. чтобы этап алгоритмизации задачи являлся одновременно и этапом программирования. Постановка задачи с использованием таблиц является четкой и недвусмысленной.
Рассмотрим таблицу решений (табл. 10.1), которая является алгоритмом проектирования элементарного технологического процесса для цилиндрических поверхностей вращения применительно к условиям некоторого завода. В зависимости от характеристик поверхности: класса точности, класса чистоты, вида термообработки и несоосности выбирается соответствующий этим характеристикам план ее обработки, т.е. операции токарная, шлифовальная и т.п. Таблица разделяется двойной горизонтальной линией на область условий и область действий. Двойной вертикальной линией таблица также разделяется на две части: в левой части находится колонка с названием “операнд” и символы операций. Справа от двойной линии размещаются колонки правила, которые содержат правые части отношений и операнды операторов (в примере - метки оператора перехода). Полученную таблицу называют таблицей принятия решений (ТР).
Таблица 10.1. Таблица принятия решений
| Операнд 1 | Оп | ||||||
| Класс - точности | ³ | ||||||
| Класс - чистоты | £ | ||||||
| Вид-термообработки | = | - | 01, | 03, | - | 01, | - |
| Несоосность | ³ | 0,1 | 0,02 | 0,01 | 0,01 | - | - |
| Перейти к | П1 | П2 | П3 | П4 | П5 | П6 |
Таблица интерпретируется следующим образом:
ЕСЛИ класс - точности >= 4
И класс - чистоты <= 6
И несоосносность >= 0.01
ТО операция 1 := токарная.
ЕСЛИ класс - точности >= 2
И класс - чистоты <= 8
И вид - термообработки 01 ИЛИ 02
И несоосносность >= 0.02
ТО операция 1:= токарная, операция 2:= шлифовальная.
Нетрудно заметить, что столбцы таблицы являются продукционными правилами.
Таблицу решений выгодно составлять в том случае, когда множество продукционных правил содержит одинаковые условия (посылки), на основе знаний которых принимаются заключения.
По сравнению с блок-схемой алгоритма, или записью на алгоритмическом языке или записью параллельных процессов в языке UML в таблице достигнута более высокая степень формализации процесса принятия решения. Она нагляднее, чем запись на алгоритмическом языке, в то же время по сравнению с блок-схемой записана на входном табличном языке.
По типу элементов в клетках ТР могут быть таблицами с ограниченными, расширенными и смешанными элементами.
В таблице с ограниченными элементами (табл. 10.2) формулировки условий являются законченными и включают переменную и значение условного выражения. Для записи элементов условий используются три символа:
ДА (условие истинно для правила);
НЕТ (условие ложно для правила);
“-“ (правило не зависит от условий).
Таблица 10.2. Группировка деталей
| Вес <30 | НЕТ | ДА | - | - |
| Диаметр > 5 | НЕТ | НЕТ | ДА | - |
| Партия > 20 | - | НЕТ | ДА | НЕТ |
| Записать в список |
Действия могут быть обозначены символами “X” (выполнить действие, указанное слева от двойной линии) или “-“ (не выполнить). Таблица смешанного вида (табл. 10.3) включает правила, в которых сочетаются как ограниченные, так и расширенные элементы. Однако каждая строка таблицы должна содержать элементы только одного вида. Например, в таблице 10.3 первая строка области условий содержит справа от двойной линии правые части отношений, которые в общем случае могут быть арифметическими или текстовыми выражениями. Вторая и третья строки области условий включают элементы ограниченного вида, т.е. логические значения ДА (истина) и НЕТ (ложь), и элемент, не влияющий на выбор решения.
Таблица10.3. Выбор операции обработки детали
| Класс чистоты | £ | - | ||||
| Наличие термообработки | = | - | НЕТ | ДА | - | - |
| Наличие хромирования | = | - | НЕТ | НЕТ | НЕТ | - |
| Операция | := | ОП1 | ОП2 | ОП3 | ОП4 | ОП5 |
Формат таблицы решений. ТР имеет заголовок, который записывается в первой строке и содержит графы ТАБЛИЦА, НОМЕР, РАЗМЕР, ИНАЧЕ, СЛЕДУЮЩАЯ. Графы разделяются вертикальными линиями. В графу ТАБЛИЦА записывается полное название таблицы и различные пояснения к ней. В графе НОМЕР указывается краткая идентификация таблицы или ее номер, например 12;ТОК:2;НОРМА. В графе РАЗМЕР записывается число строк и колонок таблицы, например 40Х20;7Х12. Графа ИНАЧЕ не заполняется, если будет выбрано хотя бы одно решение. Она служит для прекращения просмотра таблицы или указывает программе на дальнейшее действие. При этом проверяется логическая непротиворечивость входов условий и элементов таблицы. Если при заданном наборе данных не выбирается ни одно из решений, номер в этой графе указывает переход на следующую таблицу. Графа СЛЕДУЮЩАЯ заполняется в том случае, если большинство правил содержит указание перехода только в одной таблице. Это исключает необходимость писать оператор перехода на таблицу в каждом правиле. Если в правиле есть действие ПЕРЕЙТИ (номер таблицы), переход осуществляется к этой таблице, а не к таблице, номер которой указан в графе СЛЕДУЮЩАЯ.
Операторы таблиц принятия решений. Основными операторами, которые применяются в ТР, являются ПРИСВОИТЬ, ВЫЧИСЛИТЬ, ВЫПОЛНИТЬ.
Оператор ПРИСВОИТЬ указывает, что результат, полученный после выполнения действий, заданных в данной клетке, должен быть присвоен величине, приведенной в первой колонке.
Оператор ВЫЧИСЛИТЬ обеспечивает вычисление выражения, заданного в соответствующей клетке таблицы, и присваивает вычисленное значение величине, указанной в первой колонке.
Оператор ВЫПОЛНИТЬ обеспечивает выполнение обработки данных или арифметических выражений, указанных меткой, стоящей в клетке таблицы.
Область применения таблиц решений – многошаговые задачи управления объектами, где на каждом шаге требуется принять рациональное решение. Это задачи со сложной логикой принятия решений, включающие большое количество различного рода данных, каждое из которых принимает некоторое множество значений. Алгоритмизацию и программирование таких задач с различной степенью детализации целесообразно производить при помощи таблиц решений. Однако следует отметить, что создание табличного языка, не ориентированного на какой-либо алгоритмический язык, представляется нецелесообразным. Это связанно, во-первых, с разработкой средств описания алгоритмов, которые на достаточно высоком уровне уже применяются в известных алгоритмических языках. Во-вторых, такой табличный язык требует разработки транслятора, что сопряжено с большими затратами. Разработка модуля таблиц решений в рамках алгоритмического (базового) языка представляется более целесообразной.
Семантические сети
Основные понятия. В отличие от логических моделей представления знаний семантические сети позволяют успешно структурировать информацию. Граф, который лежит в основе семантической сети, собирает вокруг одного узла всю информацию по некоторому объекту. Такие модели позволяют наглядно представить круг решаемых проблем в большей степени, чем множество правил, относящихся к ним.
Семантическая сеть состоит из множества концептуальных графов. Концептуальный граф соответствует некоторой логической формуле, имена и аргументы предикатов которой изображается двумя типами узлов. Прямоугольники соответствуют аргументам, а круги - именам предикатов. Круг соединяется стрелкой с прямоугольником, если они соответствуют имени и аргументу некоторого предиката. Таким образом, прямоугольники используются для представления аргументов, событий и состояний. А круги – для увязывания этих понятий. Проиллюстрируем эти понятия на примере.
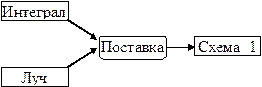 Рис. 10.1. Концептуальный граф
Рис. 10.1. Концептуальный граф
|
Пример
Логическая формула “Поставка(Интеграл,Луч,Схема_14)” формализует фразу “Завод Интеграл поставляет Схему_14 фирме Луч”. На рис. 10.1 изображен концептуальный граф для этой логической формулы. Упомянутую выше фразу можно формализовать с помощью бинарных предикатов:
Поставщик(Поставка_8, Интеграл)^
Потребитель(Поставка_8,Луч)^
Объект(Поставка_8,Схема_14)^
Элем(Поставка_8,поставки).
Концептуальный граф для этой логической формулы представлен на (рис. 10.2). Концептуальный граф n-арного предиката изображается следующим образом. Стрелка, соответствующая n-му аргументу, направлена от круга, представляющего имя предиката, к прямоугольнику, отображающему этот аргумент. Остальные прямоугольники, соответствующие первым n-1 аргументам, соединяются стрелками с кругом. Стрелки помечены номерами от 1 до n (или именами), чтобы показать соответствие между стрелкой и аргументом. Стрелки в таком графе направлены от первого аргумента к имени предиката и от имени предиката ко второму аргументу. Термины “имя предиката” и “аргумент”, представляющие соответственно функцию и концепт, часто называют “связывающий узел” и “узел-концепт” в графическом представлении.
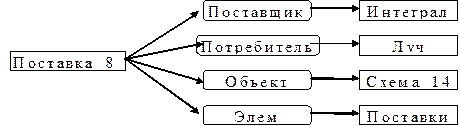 Рис. 10.2. Концептуальный граф логического представления бинарными предикатами
Рис. 10.2. Концептуальный граф логического представления бинарными предикатами
|
Начало разработки семантических сетей относится к 1960г., когда они использовались для моделирования обработки естественного языка. Так, Мастерман с помощью семантических сетей разработал 100 базовых понятий для моделирования словаря в 15000 слов.
Семантической сетью называют направленный граф с помеченными вершинами и дугами, в котором вершинам соответствуют конкретные объекты, а дугам – семантические отношения между ними. Имена вершин определяют объекты из некоторой объектной области, например, станок, робокар, деталь и т.д. Метки дуг обозначают элементы множества отношений.
В качестве примера семантической сети рассмотрим представление знаний, содержащихся в следующем предложении: "Заготовка обрабатывается на станке, после чего получается деталь, которую робот помещает в кассету; эту кассету погрузчик грузит, робокар отвозит на склад, а штабеллер помещает в ячейку". Факты обозначим кружком, понятия — прямоугольником, дуги пометим наименованиями отношений (рис. 10.3).
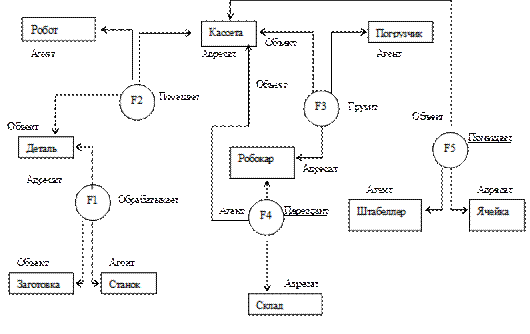
Рис. 10.3.Пример семантической сети
Семантические сети – это классический метод ИИ, используемый для представления пропозиционной информации. Семантическую сеть иногда называют пропозиционной сетью. Как обсуждалось ранее, предложение – это утверждение истинное или ложное, например, “все собаки млекопитающие” и “у треугольника 3 стороны”. Предложение – это образец декларативного знания, поскольку оно констатирует факты. Оно всегда либо истинно, либо ложно.
Структура СС графически изображена в виде узлов и векторов, соединяющих их. Узлы обычно рассматриваются как объекты, а вектора как соединения или ограничения.
Соединения в СС нужны для выражения отношений. Узлы в основном используются для представления физических лиц, ситуаций или понятий. На рис 10.4 показана СС в виде прямолинейного графика, где линии указывают на родственные связи между членами семьи. Отношения в СС обеспечивают основу при систематизации знаний. Без отношений между объектами знание – это просто собрание бессвязных фактов. А при наличии отношений, знание выглядит как единая система, которая может быть следствием других сведений.
СС иногда рассматриваются как ассоциативные сети, потому что все узлы ассоциативны или связаны между собой. Первоначально СС фактически моделировали человеческую память в виде ассоциативной сети. Понятия представлялись узлами, которые соединялись линиями. Согласно такой модели, когда мы читаем слова в предложении и улавливаем суть, активизируются отношения между словами. Если мы получим достаточно информации о другом понятии, то вся идея в целом приобретет смысл.
Отдельные виды отношений доказали свою пользу в разнообразии представлений о знании. Прежде, чем установить новые представления по различным вопросам, часто используют обычные виды СС. Это помогает людям разобраться в незнакомой сети.
На СС часто используются соединений ISA (IS-A - это есть) и AKO (A-KIND-OF- в виде). Рис. 10.5 является примером СС с использованием этих соединений. Пометка на рисунке означает, что объекты, принадлежащие к классу, связаны между собой определенными отношениями. Например, возьмем ряд объектов: 3, яйца, синий, шины, искусство.
Элементы этого множества не имеют отношений между собой. Напротив, классы самолетов, поездов и автомобилей связаны, так как они представляют виды транспорта.
Соединение AKO используется для указания одного класса с другим. Мы не пользуемся АКО, чтобы установить отношения между определенными людьми, так как этой функцией обладает ISA. А АКО связывает классы детей и родителей.
|
Рис.3.6. Семантическая сеть «Семейные связи»

Рис. 10.4. Семантическая сеть представления семейных отношений
Общий класс, который соединяется с другими посредством АКО, называется высшим классом. Если от высшего класса соединяющая АКО направлена к следующему узлу, то этот класс будет уже подчиняться новому суперклассу. Другой способ выражения отношений, это когда соединение АКО направлено от подкласса к классу.
Предметы в классе имеют один или более общих признаков. Каждый признак имеет смысловое значение. При сочетании признака и значения получаем свойство. Например, автомобиль имеет признаки: размер, цвет, мощность, вес и т.п. Значение признака фигуры эллипсоидное.
Дублирование одной характеристики посредством передачи ее от предыдущего объекта называется наследованием свойств. Предполагается, что все члены класса наследуют свойства суперклассов. Наследование свойств занимает главенствующую позицию. Оно является полезным инструментом представления знаний, поскольку устраняет необходимость повторять свойства. Поскольку представление сложных отношений требует минимизации количества соединений и узлов, то наследование свойств и система соединений являются эффективным средством представления знаний.
Рассмотрим более широкое определение семантической сети. Пусть задано конечное множество атрибутов A={A1,...,An} и конечное множество отношений R= {R1,...,Rm}. Схемой, или интенсионалом, отношения R называют набор пар INT(Ri)={...[Aj,DOM(Aj)],...}, где Ri – имя отношения; DOM(Aj) – домен Aj, т.е. множество значений атрибута Aj отношения Ri.
Объединение всех доменов называют базовым множеством модели, или множеством объектов, на которых задаются отношения Ri. Экстенсионалом отношения Ri называют множество EXT(Ri)={F1,...,Fp}, где Fr,r = 1,..,p, - факт отношения Ri. Факт задается совокупностью пар вида атрибут-значение, называемых атрибутивными парами. Под фактом понимают конкретное содержание отношения между объектами. Факт - это подграф семантической сети, имеющий звездообразную структуру. Корень подграфа - вершина предикативного типа, помеченная уникальной меткой, включающая имя соответствующего отношения.
Объекты и отношения. В семантических сетях используются четыре основных типа объектов: понятия, события, свойства и значения. Понятия представляют собой сведения об абстрактных или физических объектах предметной области. Они могут быть заданы множеством доменов (параметров или констант).
События - это действия, которые могут перевести предметную область из текущего состояния в некоторое новое. Можно перевести предметную область в определенное желаемое (целевое) состояние, поставить задачу, отыскать на семантической сети путь событий, приводящих к целевому состоянию.
Свойстваиспользуются для характеристики (уточнения) понятий, событий, процессов и т.д. Свойствами понятий могут быть цвет, размеры, качество, а свойствами действий - время, продолжительность, место и т.д.
Значения - это значения из какого-нибудь множества, которые могут принимать свойства.
На рис. 10.5 представлен пример семантической сети для моделирования закладной под кредит.
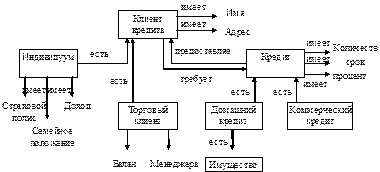
Рис. 10.5. Семантическая сеть для моделирования закладной под кредит
Трудности, возникающие с семантическими сетями. Хотя семантические сети могут быть очень полезны в представлении знаний, они имеют ограничения, такие как отсутствие стандартов наименований направленных линий. Дополнительной проблемой является наименование узлов. Если узел помечен “кафедра”, например:
Дата добавления: 2016-10-26; просмотров: 6170;











