Основные теоретические выводы

· Объекты(предметы, явления, процессы) могут обладать особыми свойствами, которые называются величинами.

· Свойство можно было считать величиной, если оно удовлетворяет ряду условий:

- Для величин одного рода имеют место отношения «равно», «меньше» и «больше», и для любых величин А и В справедливо одно и только одно из отношений: А < B, A = B, A > B.

- Отношение «меньше» для однородных величин транзитивно:

если А < B и В < С, то А < С.

- Величины одного рода можно складывать, в результате сложения получается величина того же рода. Иными словами, для любых двух величин А и В однозначно определяется величина С=А+В, которую называют суммой величин А и В.

- Величины одного рода можно вычитать, получая в результате величину того же рода. Определяют вычитание через сложение.

- Разностью величин А и В называется такая величина С=А-В, что А=В+С.

- Разность величин А и В существует тогда и только тогда, когда А > В.

· Величину можно умножать на положительное действительное число, в результате получают величину того же рода. Более точно, для любой величины А и любого положительного действительного числа х существует единственная величина В= х × А, которую называют произведением величины А на число х.

· Величины одного рода можно делить, получая в результате число. Определяют деление через умножение величины на число.

· Частным величин А и В называется такое положительное действительное число х = А : В, что А= х × В

· Величины как свойства объектов проявляются при их сравнении, причем для каждой величины существует свой способ сравнения. Если выбрана единица величины, то величину можно измерить. В результате измерения получается число, которое называют численным значением величины или мерой величины при выбранной единице величины.

· Введены записи Х= а×E и а = m_E (Х), в которых Х – обозначает величину, E - единицу величины, а – действительное число.

Практическая часть

1. О каких величинах идет речь в следующих предложениях:

а) Груши дороже яблок.

б) Книга тяжелее тетради.

в) Таня выше Светы.

2. Какие величины могут характеризовать следующие объекты:

а) карандаш; б) человек; в) озеро?

3. Имеются два куска проволоки. Каким образом можно сравнить их длины, не прибегая к измерению? Какими могут быть результаты сравнения?

4. Как можно сравнить массы двух предметов, не определяя массу каждого из них? Какими могут быть результаты сравнения?

5. На рисунке 1 изображены два прямо­угольника, имеющие площади А и В.

А В

Постройте прямоугольник, площадь которого равна: а) А+В; б) 3×А; в) 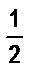×В; г) В–А.

6. Разбейте на классы тремя способами сле­дующие величины:

А - высота дерева; М - площадь доски;

В - 16кг; Н – 13с;

С - масса доски; К - 26м;

Д - 25 см; L - длина веревки;

Е - возраст дерева; Р - толщина доски.

7. Назовите стандартные единицы, с помощью которых можно измерить величины, указанные в таблице. Запишите их.

8. О каких величинах идет речь в следующих предложениях:

а) В одной коробке 25 яблок, а в другой 30 яблок.

б) 15 яблок дороже, чем 8 груш.

в) В одном ящике 20 кг овощей, а в другом 12 кг овощей.

9. Какие из данных величин можно сравнить между собой:

1500м; 2,5 км; 18 штук; 8 десятков;

3ц; 1км 500м; 299 кг; 18 пар.

10. Сравните величины:

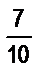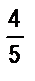а) 56 мин и ч; б) м и дм;

в) 1,5 см и 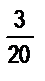дм; г) 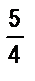кг и 1250 г.

11. Назовите объект, его величину, численное значение и единицу измерения величины в каждом из следующих предложений:

а) В коробке 8 кг яблок.

б) Глубина оврага 2 м.

в) Площадь садового участка 6 соток.

г) В сервизе 6 тарелок.

д) Рост девочки 1 м 20 см.

12. Назовите величины и объекты, о которых говорится в задаче:

а) За тетради заплатили х р., а за карандаши на t р. меньше. Сколько стоили карандаши?

б) Мешок картофеля тяжелее ящика с луком на 2 кг. Какова масса мешка картофеля, если масса ящика с луком z кг?

в) На первой полке стояло х книг. На второй на у книг больше, а на третьей на y книг меньше, чем на первой полке. Сколько книг стояло на трех полках?

13. Назовите величины, о которых говорится в задаче, и действия с ними, которые будут выполнены в процессе решения:

а) В ящике было 24 кг апельсинов. Сначала из него взяли 5 кг, а потом в 3раза больше, чем в первый раз. Сколько апельсинов осталось в ящике?

б) Для вышивания первого узора нужно 24 м ниток, для второго в 6 раз меньше, а для третьего - на 16м больше, чем для первого. Хватит ли 7 катушек для вышивания всех узоров, если в каждой катушке по 10 м ниток?

14. Решите задачи, предварительно установив, в чем их сходство и различие:

а) Со склада отправили в столовую и в магазин 8 машин с овощами. Магазин получил 24 т овощей, а столовая - в 3 раза меньше. Сколько машин с овощами отправили в магазин и сколько в столовую, если масса овощей в каждой машине была одинаковой?

б) Со склада отправили в столовую и в магазин несколько машин с овощами. Масса овощей в каждой машине была одинаковой. Магазин получил 24 т овощей, а столовая - в 3 раза меньше. Сколько машин с овощами отправили со склада, если в столовую отправили 2 машины?