Ключевое слово this

Методу объекта необходим доступ к информации, которая хранится в объекте, чтобы выполнить с ней какие – то действия (в соответствии с назначением метода). Например, коду внутри user.sayHi() может понадобиться имя пользователя, которое хранится а объекте user.

Для доступа к информации внутри объекта метод может использовать ключевое слово this. Значение this – это объект «перед точкой», который использовался для вызова метода.

Ключевое слово this не используется в стрелочных функциях.

Тема 2.2 Продвинутая работа с функциями

Рекурсия и стек

Рекурсия – это прием программирования, когда задача разбивается на несколько аналогичных, но более простых задач. В процессе выполнения задачи в теле функции могут быть вызваны другие функции для выполнения подзадач. Частный случай подвызова – когда функция вызывает саму себя. Это как раз и называется рекурсия.

В качестве примера создадим функцию pow(x, n), которая возводит х в степень n.

pow(2, 2) = 4

pow(2, 3) = 8

pow(2, 4) = 16

Рассмотрим два способа решения этой задачи:

1. итерационный способ (через цикл for):

function pow(x, n) {

let result = 1;

// умножаем result на x n раз в цикле

for (let i = 0; i < n; i++) {

result *= x;

}

return result;

}

alert( pow(2, 4) ); // 16

2. Рекурсивный способ:

function pow(x, n) {

if (n == 1) {

return x;

} else {

return x * pow(x, n - 1);

}

}

alert( pow(2, 4) ); // 16

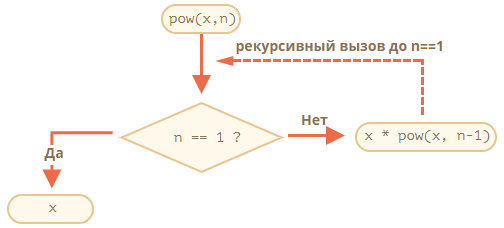
Рекурсивный вариант отличается принципиально: когда функция pow(x, n) вызывается, исполнение делится на две ветви:

if n==1 = x

/

pow(x, n) =

\

else = x * pow(x, n - 1)

1. Если n ==1, все просто, это ветвь называется базой рекурсии, потому что сразу приводит к очевидному результату: pow(x, n) равно х.

2. Мы можем представить pow(x, n) в виде: x * pow(x, n – 1.В математике это записывалось бы как xⁿ = x * x^n-1. Эта ветвь – шаг рекурсии: мы сводим задачу к более простому действию (умножению на х) и более простой аналогичной задаче (pow с меньшим n). Последующие шаги упрощают задачу все больше и больше, пока n не достигнет 1.

Говорят, что функция pow рекурсивно вызывает саму себя до n ==1.

Замыкания

Замыкания (closure) представляют собой конструкцию, когда функция, созданная в одной области видимости, запоминает свое лексическое окружение даже в том случае, когда она выполняется вне своей области видимости.

Замыкания включают три компонента:

1. Внешнюю функцию, которая определяет некоторую область видимости и в которой определены некоторые переменные – лексическое окружение;

2. Переменные (лексическое окружение), которые определены во внешней функции;

3. Вложенную функцию, которая использует эти переменные.

function outer(){ // внешняя функция

let n; // некоторая переменная

return inner(){ // вложенная функция

// действия с переменной n

}

}

Рассмотрим замыкания на примере:

<script>

function outer(){

let x = 5;

function inner(){

x++;

document.write(x + '<br>');

}

return inner;

}

let fn = outer(); // fn = inner, так как функция outer возвращает функцию inner

// вызываем внутреннюю функцию inner

fn(); //6

fn(); //7

</script>

В примере функция outer задает область видимости, в которой определены внутренняя функция inner и переменная x. Переменная x представляет лексическое окружение для функции inner. В самой функции inner производим инкремент переменной x и выводим ее значение в браузер. В конце функция outer возвращает функцию inner.

Далее вызываем функцию outer:

let fn = outer();

Поскольку функция outer возвращает функцию inner, то переменная fn будет хранить ссылку на функцию inner. При этом функция запомнила свое окружение, т.е. переменную х.

Далее можно несколько раз вызвать функцию inner, которая будет производить инкремент.

Таким образом, несмотря на то, что переменная х определена вне функции inner, эта функция запомнила свое окружение и может его использовать, несмотря на то, что вызывается она вне функции outer, в которой была определена. В этом и заключается суть замыкания.