Сдвиговые регистры с обратной связью по переносу
Сдвиговый регистр с обратной связью по переносу, или FCSR (feedback with carry shift register), похож на LFSR. В обоих есть сдвиговый регистр и функция обратной связи, разница в том, что в FCSR есть также регистр переноса (см. Рис. 17-3). Вместо выполнения XOR над всеми битами отводной последовательности эти биты складываются друг с другом и с содержимым регистра переноса. Результат mod 2 и становится новым битом. Результат, деленный на 2, становится новым содержимым регистра переноса.

Рис. 17-3. Сдвиговый регистр с обратной связью по переносу.
На Рис. 17-4 приведен пример 3-битового FCSR с ответвлениями в первой и второй позициях. Пусть его начальное значение 001, а начальное содержимое регистра переноса равно 0. Выходом будет является крайний правый бит сдвигового регистра.
| Сдвиговый регистр | Регистр переноса |
| 0 0 1 | |
| 1 0 0 | |
| 0 1 0 | |
| 1 0 1 | |
| 1 1 0 | |
| 1 1 1 | |
| 0 1 1 | |
| 1 0 1 | |
| 0 1 0 | |
| 0 0 1 | |
| 0 0 0 | |
| 1 0 0 |
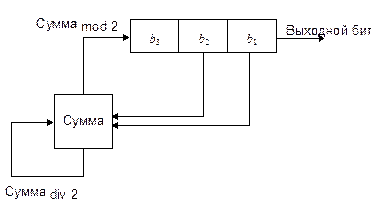
Рис. 17-4. 3-битовый FCSR.
Заметим, что конечное внутреннее состояние (включая содержимое регистра переноса) совпадает со вторым внутренним состоянием. С этого момента последовательность циклически повторяется с периодом, равным 10.
Стоит упомянуть и еще о нескольких моментах. Во первых, регистр переноса является не битом, а числом. Размер регистра переноса должен быть не меньше log2t, где t - это число ответвлений. В предыдущем примере только три ответвления, поэтому регистр переноса однобитовый. Если бы было четыре ответвления, то регистр переноса состоял бы из двух битов и мог принимать значения 0, 1, 2 или 3.
Во вторых, существует начальная задержка прежде, чем FCSR перейдет в циклический режим. В предыдущем примере никогда не повторяется только одно состояние. Для больших и более сложных FCSR задержка может быть больше.
В третьих, максимальный период FCSR не 2n-1, где n- длина сдвигового регистра. Максимальный период равен q-1, где q- это целое число связи. Это число задает ответвления и определяется как:
q= 2ql + 22q2 + 23q3 + . . . + 2nqn-1
(Да, qiотсчитываются слева направо.) И даже хуже, qдолжно быть простым числом, для которого 2 является примитивным корнем. В дальнейшем предполагается, что q удовлетворяет этому условию.
В приведенном примере q= 2*0 + 4*1 + 8*1 - 1 == 11. 11 - это простое число, примитивным корнем которого является 2. Роэтому максимальный период равен 10.
Не все начальные состояния дают максимальный период. Например, рассмотрим FCSR с начальным значением 101 и регистром переноса, установленным в 4.
| Сдвиговый регистр | Регистр переноса |
| 1 0 1 | |
| 1 1 0 | |
| 1 1 1 | |
| 1 1 1 |
С этого момента регистр выплевывает бесконечную последовательность единиц.
Любое начальное состояние приводит к одной из четырех ситуаций. Во первых, оно может быть частью максимального периода. Во вторых, оно может перейти в последовательность максимального периода после начальной задержки. В третьих, после начальной задержки оно может породить бесконечную последовательность нулей. В четвертых, после начальной задержки оно может породить бесконечную последовательность единиц.
Для определения, чем закончится конкретное начальное состояние, существует математическая формула, но намного проще проверить это опытным путем. Запустите на некоторое время FCSR. (Если m- это начальный объем памяти, а t- количество ответвлений, то достаточно log2(t) + log2(m) +1 тактов.) Если выходной поток вырождается в бесконечную последовательность нулей или единиц за nбитов, где n- это длина FCSR, не используйте это начальное состояние. В противном случае его можно использовать. Так как начальное состояние FCSR соответствует ключу потокового шифра, это означает, что ряд ключей генератора на базе FCSR будут слабыми.
В Табл. 17-1 перечислены все целые числа связи, меньшие 10000, для которых 2 является примитивным корнем. Для всех этих чисел максимальный период равен q-1. Чтобы получить по одному из этих чисел последовательность ответвлений, рассчитаем бинарный состав q+1. Например, 9949 дает последовательность ответвлений в позициях 1, 2, 3, 4, 6, 7, 9, 10 и 13, так как
9950 = 213 + 210 + 29 + 27+ 26 + 24 + 23+ 22 + 21
В Табл. 17-2 перечислены все отводные последовательности из четырех ответвлений, которые дают FCSR максимальной длины для сдвиговых регистров с длиной 32 бита, 64 бита и 128 битов. q, простое число, примитивным корнем которого является 2, получается объединением всех четырех значений, a, b, c и d.
q = 2a + 2b + 2c + 2d - 1
Для создания FCSR с периодом q- 1 можно использовать любую из этих последовательностей.
Идея использовать в криптографии FCSR все еще является очень новой, впервые она была выдвинута Энди Клаппером (Andy Klapper) и Марком Горески (Mark Goresky) [844, 845, 654, 843, 846]. Также, как анализ LFSR основан на сложении примитивных многочленов mod 2, анализ FCSR основан на сложении неких чисел, называемых 2-adic. Соответствующая теория выходит далеко за пределы этой книги, но в мире 2-adic чисел существуют аналоги для всего. Точно также, как определяется линейная сложность, можно определить и 2-adic сложность. Существует 2-adic аналог и для алгоритма Berlekamp-Massey. Это означает, что перечень возможных потоковых шифров по крайней мере удвоился. Все, что можно делать с LFSR, можно делать и с FCSR.
Существуют работы, развивающие эту идею и рассматривающие несколько регистров переноса. Анализ этих генераторов последовательностей основан на сложении разветвленных расширений 2-adic чисел [845, 846].
Дата добавления: 2021-01-26; просмотров: 704;











