Проверка допустимой нагрузки двигателя по нагреву методом средних потерь
 Нагрузка многих механизмов, работающих в длительном режиме, является переменной. Температура двигателя при этом непрерывно изменяется. Проверка правильности выбора мощности двигателя в этом случае должна производиться путем определения наибольшей температуры перегрева tмакс и сравнения ее с tдоп. При этом tмакс должна быть £tдоп. Таким образом, проверка на перегрев требует определения tмакс, что связано с построением температурной кривой. Это можно было бы сделать путем замены кривой нагрузки, например, I=f(t) ступенчатой с постоянной нагрузкой на отдельных ступенях, как это изображено на рисунке. При этих условиях закон изменения температуры перегрева на любом участке будет
Нагрузка многих механизмов, работающих в длительном режиме, является переменной. Температура двигателя при этом непрерывно изменяется. Проверка правильности выбора мощности двигателя в этом случае должна производиться путем определения наибольшей температуры перегрева tмакс и сравнения ее с tдоп. При этом tмакс должна быть £tдоп. Таким образом, проверка на перегрев требует определения tмакс, что связано с построением температурной кривой. Это можно было бы сделать путем замены кривой нагрузки, например, I=f(t) ступенчатой с постоянной нагрузкой на отдельных ступенях, как это изображено на рисунке. При этих условиях закон изменения температуры перегрева на любом участке будет
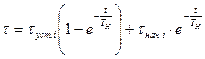 , где
, где
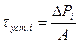 - установившаяся температура, соответствующая потерям ∆Pi на iой ступени, а tнач.i - начальная температура на этой ступени. Кривая нагрева t=f(t) на всех ступенях определится, если известна начальная t на любом из участков, т.к. это полностью определяет температуру во всех точках этого участка, в том числе и в его конце, а значит и в начале следующего участка.
- установившаяся температура, соответствующая потерям ∆Pi на iой ступени, а tнач.i - начальная температура на этой ступени. Кривая нагрева t=f(t) на всех ступенях определится, если известна начальная t на любом из участков, т.к. это полностью определяет температуру во всех точках этого участка, в том числе и в его конце, а значит и в начале следующего участка.
Однако метод построения кривой нагрева требует большого числа вычислений и построений. Кроме того, необходимо знать постоянную ТН, которая обычно неизвестна да и зависит от условий охлаждения. Поэтому на практике применяют хотя и менее точный, но более простой метод – метод средних потерь. Сущность его заключается в нахождении средних потерь в двигателе ∆Pср при заданном графике нагрузки и сравнении их с номинальными потерями, на которые двигатель рассчитан при длительном режиме работы. При этом предполагается, что при равенстве ∆Pср=∆Pн двигатель будет работать с допустимой для него температурой, т.к.
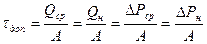 .
.
 Рассмотрим процесс нагрева двигателя, работающего по некоторому циклическому графику. По истечение большего числа циклов двигатель достигнет установившегося теплового состояния. При этом температура нагрева изоляции будет одинаковой как в начале, так и в конце цикла, а в промежутке будет изменяться по установившемуся экспоненциальному закону. При небольшой длительности цикла по сравнению с ТН отклонение температуры за tц от начального и конечного значений будет невелико. Это дает основание максимальным значением температуры перегрева считать ее значение в начале и в конце цикла. Температура перегрева в конце последнего участка цикла может быть получена, если записать ряд последовательных значений температур перегрева в конце каждого из участков цикла работы:
Рассмотрим процесс нагрева двигателя, работающего по некоторому циклическому графику. По истечение большего числа циклов двигатель достигнет установившегося теплового состояния. При этом температура нагрева изоляции будет одинаковой как в начале, так и в конце цикла, а в промежутке будет изменяться по установившемуся экспоненциальному закону. При небольшой длительности цикла по сравнению с ТН отклонение температуры за tц от начального и конечного значений будет невелико. Это дает основание максимальным значением температуры перегрева считать ее значение в начале и в конце цикла. Температура перегрева в конце последнего участка цикла может быть получена, если записать ряд последовательных значений температур перегрева в конце каждого из участков цикла работы:
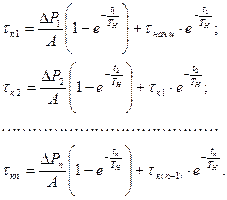
Если в этой системе исключить значения температур перегрева в конце каждого промежуточного участка при i<n, то температура перегрева в конце последнего участка цикла будет
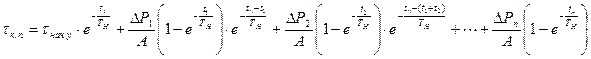
или т.к. 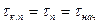 , получим
, получим
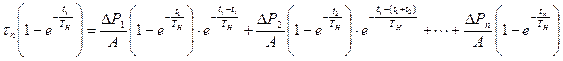 .
.
Выразив tn через средние потери, получим
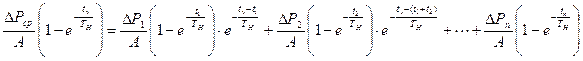 .
.
Это выражение говорит о том, что процесс нагрева двигателя при меняющейся нагрузке, можно заменить некоторым режимом с постоянной нагрузкой, создающим тот же нагрев. Для определения потерь ∆Pср, соответствующих длительному режиму с постоянной нагрузкой, разложим все экспоненциальные функции в ряд Маклорена ( 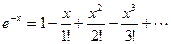 ), пренебрегаем всеми членами ряда кроме первых двух и получим
), пренебрегаем всеми членами ряда кроме первых двух и получим
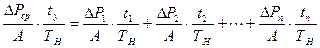 .
.
Предполагая, что двигатель работает с постоянной скоростью, следовательно, неизменными А и ТН, получим
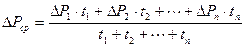 .
.
Условием правильности выбора является ∆Pср£∆Pн. В случае существенного расхождения в величинах ∆Pср и ∆Pн, необходимо выбрать больший по мощности двигатель и провести все расчеты заново.
Следует также иметь в виду, что условие ∆Pср£∆Pн справедливо лишь в случае, когда двигатель должен работать при температуре окружающей среды +40°С. Если она отличается от +40°С, условие проверки мощности предварительно выбранного двигателя будет таким:
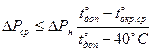 .
.
Выражение для ∆Pср справедливо для двигателей, имеющих независимую вентиляцию и с самовентиляцией, работающих с постоянной скоростью. Для двигателей с самовентиляцией и охлаждаемых естественным путем, работающих с переменной скоростью, в выражение для ∆Pср необходимо внести поправки, учитывающие ухудшение условий охлаждения при изменении скорости и во время пауз. Внесение поправок удобно рассмотреть на примере работы двигателя по трехпериодной тахограмме (см. рисунок).
 При работе с установившейся скоростью количество тепла, отдаваемого в окружающую среду
При работе с установившейся скоростью количество тепла, отдаваемого в окружающую среду 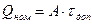 . Во время паузы
. Во время паузы 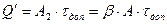 где
где 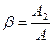 - коэффициент, учитывающий ухудшение условий охлаждения во время паузы. Во время переходных процессов (пуск, торможение, изменение скорости) коэффициент теплоотдачи в окружающую среду принимается равным
- коэффициент, учитывающий ухудшение условий охлаждения во время паузы. Во время переходных процессов (пуск, торможение, изменение скорости) коэффициент теплоотдачи в окружающую среду принимается равным
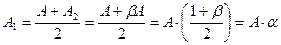 , где
, где 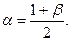
Для ДПТ a=0,75; для АД a=0,5. Выражение для определения средних потерь принимает теперь вид (применительно к трехпериодной тахограмме):
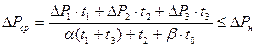 .
.
Метод средних потерь хотя и является одним из наиболее точных, основанных на учете среднего нагрева двигателя, не учитывает, однако, максимальную температуру при переменном графике нагрузки и не дает возможности выбрать двигатель по нагрузочной диаграмме, т.к. для определения ∆Pi необходимо знать параметры двигателя. Кроме того, этот метод не всегда удобен вследствие трудности расчета потерь мощности. Поэтому на практике применяются другие методы оценки нагрева двигателя.
Определение потерь и КПД двигателя при номинальной и неноминальной нагрузке
Полные номинальные потри мощности
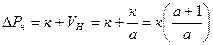 , где
, где 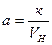 - коэффициент потерь.
- коэффициент потерь.
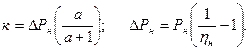
Полные потери при неноминальной нагрузке
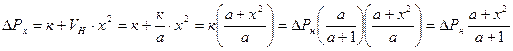 .
.
КПД при неноминальной нагрузке (х – коэффициент загрузки двигателя по току или мощности):
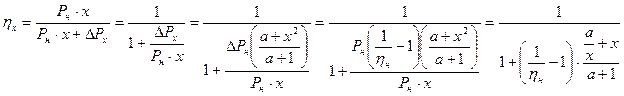
Дата добавления: 2019-09-30; просмотров: 597;











