Измерительные шкалы

В основе любого наблюдения и анализа лежат измерения. Измерение - это алгоритмическая операция, которая данному наблюдаемому состоянию объекта ставит в соответствие определенное обозначение: число, номер или символ. Обозначим через х_i наблюдаемое состояние (свойство) объекта, а через у_i - обозначение для этого свойства (где i=1, 2, …, m). Чем теснее соответствие между состояниями и их обозначениями, тем больше информации можно извлечь в результате обработки данных. Менее очевидно, что степень этого соответствия зависит не только от организации измерений (т. е. от экспериментатора), но и от природы исследуемого явления, и что сама степень соответствия в свою очередь определяет допустимые (и недопустимые) способы обработки данных.

Множество обозначений, используемых для регистрации состояний наблюдаемого объекта, называется измерительной шкалой. Для измерения различных свойств объектов применяют различные шкалы. В общем случае под шкалой понимается упорядоченное множество проявлений свойств объекта (качественных или количественных), отображенное на упорядоченное множество чисел или других условных знаков.

Измерительные шкалы в зависимости от допустимых на них операций различаются по их силе. Самые слабые - номинальные шкалы, а самые сильные - абсолютные.

●Шкала физических величин – это упорядоченная последовательность значений физической величины, принятая по соглашению сторон на основании точных измерений.

С нормативной информацией о шкалах можно познакомиться в МИ 2365-96 «ГСОЕИ. Шкалы измерений. Основные положения. Термины и определения» (методическая инструкция).

●Шкалированиепредставляет собой отображение какого-либо свойства объекта или явления в числовом множестве.

Можно сказать, что чем сильнее шкала, в которой производятся измерения, тем больше сведений об изучаемом объекте, явлении, процессе дают измерения. Поэтому так естественно стремление каждого исследователя провести измерения в возможно более сильной шкале. Однако важно иметь в виду, что выбор шкалы измерения должен ориентироваться на объективные отношения, которым подчинена наблюдаемая величина, и лучше всего производить измерения в той шкале, которая максимально согласована с этими отношениями. Можно измерять и в шкале более слабой, чем согласованная (это приведет к потере части полезной информации), но применять более сильную шкалу опасно: полученные данные на самом деле не будут иметь той силы, на которую ориентируется их обработка.

Выделяют три основных атрибута измерительных шкал, наличие или отсутствие которых определяет принадлежность шкалы к той или иной категории:

1. Упорядоченность данных означает, что один пункт шкалы, соответствующий измеряемому свойству, больше, меньше или равен другому пункту;

2. Интервальность пунктов шкалы означает, что интервал между любой парой чисел, соответствующих измеряемым свойствам, больше, меньше или равен интервалу между другой парой чисел;

3. Нулевая точка (или точка отсчета) означает, что набор чисел, соответствующих измеряемым свойствам, имеет точку отсчета, обозначаемую за ноль, что соответствует полному отсутствию измеряемого свойства.

Все шкалы можно разделить на 2 группы:

1. Качественные или неметрические шкалы, в которых отсутствуют единицы измерений (номинальная и порядковая шкалы);

2. Количественные или метрические (шкала интервалов, шкала отношений и абсолютная шкала).

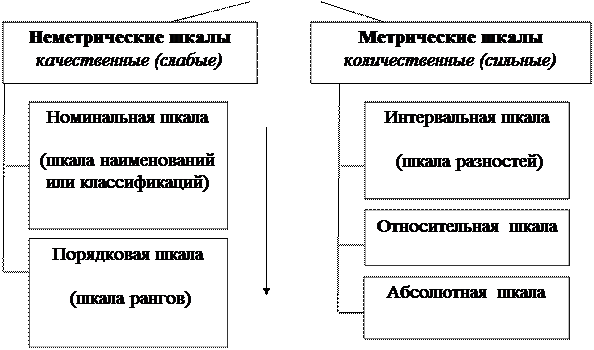Виды шкал

I. Шкалы наименований (номинальная или классификационная) применяются для объектов, свойства которых проявляются только в отношении эквивалентности

Шкала представляет собой конечный набор обозначений для никак не связанных между собой состояний (свойств) объекта (рис. 1).

Здесь отсутствуют все главные атрибуты измерительных шкал, а именно упорядоченность, интервальность, нулевая точка.

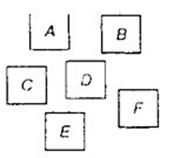
Рис. 1. Номинальная шкала.

Измерение будет состоять в том, чтобы, проведя эксперимент над объектом, определить принадлежность результата к тому или иному состоянию и записать это с помощью символа (набора символов), обозначающего данное состояние. Это самая простая шкала из тех, что могут рассматриваться как измерительные, хотя фактически эта шкала не ассоциируется с измерением и не связана с понятием «величина». Она используется только с целью отличить один объект от другого.

Пр: атлас цветов, шкала запахов и т.п.

Допустимые операции, выполняемые с величинами:

= или ≠

Операции > или < недопустимы!

Если классифицируются дискретные по своей природе объекты и явления, то естественнее всего использовать шкалу наименований.

Примеры:

Для обозначения измеряемого (или оцениваемого) свойства в номинальной шкале могут быть использованы:

· слова естественного языка (например, географические названия, собственные имена людей и т. д.);

· произвольные символы (гербы и флаги государств, эмблемы родов войск, всевозможные значки и т.д.);

· номера (регистрационные номера автомобилей, официальных документов, номера на майках спортсменов);

· их различные комбинации (например, почтовые адреса, экслибрисы личных библиотек, печати и пр.).

Однако необходимость классификации возникает и в тех случаях, когда классифицируемые состояния образуют непрерывное множество (или континуум). Задача сводится к предыдущей, если все множество разбить на конечное число подмножеств, искусственно образуя тем самым классы эквивалентности; тогда принадлежность состояния к какому-либо классу снова можно регистрировать в шкале наименований. Однако условность введенных классов (не их шкальных обозначений, а самих классов) рано или поздно проявится на практике.

Примеры:

1. Например, возникают трудности точного перевода с одного языка на другой при описании цветовых оттенков: в английском языке голубой, лазоревый и синий цвета не различаются.

2. Названия болезней также образуют шкалу наименований. Психиатр, ставя больному диагноз «шизофрения», «паранойя», «маниакальная депрессия» или «психоневроз», использует номинальную шкалу; и все же иногда врачи не зря вспоминают, что «нужно лечить больного, а не болезнь»: название болезни лишь обозначает класс, внутри которого на самом деле имеются различия, так как эквивалентность внутри класса носит условный характер.

Необходимо понимать, что обозначения классов — это только символы, даже если для этого использованы номера. С этими номерами нельзя обращаться как с числами — это только цифры.

Пример: Если у одного спортсмена на спине номер 1, а другого — 2, то никаких других выводов, кроме того, что это разные участники соревнований, делать нельзя: например, нельзя сказать, что «второй в два раза лучше».

При обработке экспериментальных данных, зафиксированных в номинальной шкале, непосредственно с самими данными можно выполнять только операцию проверки их совпадения или несовпадения.