Токи в полупроводниках
Как известно, электрическим током называется направленное движение свободных носителей заряда. В полупроводниках имеются два типа носителей заряда – электроны и дырки. Поэтому ток в полупроводнике имеет две составляющие – электронную и дырочную. При этом движение электронов и дырок может вызываться двумя причинами. Первой причиной является электрическое поле. Направленное движение частиц под действием электрического поля называется дрейфом. Соответственно ток, который переносят при этом электроны и дырки называется дрейфовым током или током проводимости. Второй причиной направленного движения частиц является их неравномерное распределение в полупроводнике. Движение частиц вследствие неравномерного их распределения называется диффузией и никак не связано с зарядом частиц. Ток, который при этом переносят частицы, называется диффузионным током.
Следует иметь в виду, что за направление электрического тока принято направление движения положительно заряженных частиц. Поэтому направление дырочных составляющих как дрейфового, так и диффузионного тока совпадают с направлением движения дырок. Электроны же, как отрицательно заряженные частицы, создают ток направленный навстречу их движению.
Под действием электрического поля отрицательно заряженные электроны и положительно заряженные дырки движутся в противоположных направлениях. При этом с учетом вышесказанного электронная и дырочная составляющие дрейфового тока совпадают по направлению. В относительно слабых электрических полях (Е  ) дрейфовые скорости электронов и дырок (усредненные скорости их направленного движения под действием электрического поля) пропорциональны напряженности электрического поля
) дрейфовые скорости электронов и дырок (усредненные скорости их направленного движения под действием электрического поля) пропорциональны напряженности электрического поля
 =
= 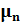 E, (1.15)
E, (1.15)
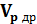 =
= 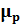 E. (1.16)
E. (1.16)
Коэффициенты пропорциональности 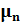 и
и 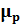 называются подвижностями электронов и дырок соответственно. В силу различного характера движения электронов и дырок подвижность электронов оказывается выше подвижности дырок (
называются подвижностями электронов и дырок соответственно. В силу различного характера движения электронов и дырок подвижность электронов оказывается выше подвижности дырок ( 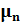

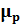 ). В разных материалах подвижности электронов и дырок различны.
). В разных материалах подвижности электронов и дырок различны.
Плотность дрейфового тока (сила тока, отнесенная к площади поперечного сечения потока частиц), переносимого электронами и дырками,
пропорциональна их скорости и концентрации
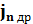 =
=  =
= 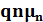 E,(1.17)
E,(1.17)
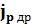 =
= 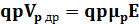 ,(1.18)
,(1.18)
где 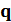 -взятый по модулю заряд электрона.
-взятый по модулю заряд электрона.
Складывая (1.17) и (1.18) получаем выражение для суммарной плотности дрейфового тока
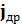 =
= 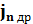 +
+  = q
= q 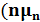 + p
+ p 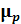 )E =
)E = 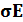 , (1.19)
, (1.19)
где в качестве коэффициента пропорциональности между напряженностью поля и плотностью дрейфового тока выступает удельная электрическая проводимость полупроводника 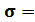 q
q 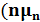 + p
+ p 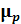 ). Заметим, что выражение (1.19) представляет собой дифференциальную форму закона Ома.
). Заметим, что выражение (1.19) представляет собой дифференциальную форму закона Ома.
Важно установить от чего зависят удельные электрические проводимости собственного и примесных полупроводников. В собственном полупроводнике ni=pi , поэтому
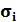 = q
= q 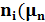 +
+ 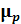 ). (1.20)
). (1.20)
В примесных полупроводниках, поскольку nn >> pnи pp >> np, можно пренебречь вкладом в дрейфовый ток неосновных носителей. Тогда учитывая, что 
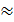 NDи
NDи 
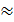 NA, получаем
NA, получаем
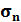
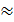 q
q  , (1.21)
, (1.21)

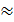 q
q  . (1.22)
. (1.22)
Отметим, что подвижность частиц изменяется довольно слабо (подробнее об этом чуть ниже). Поэтому в собственном полупроводнике удельная электрическая проводимость определяется в основном температурой, поскольку именно от нее экспоненциально зависит собственная концентрация. В примесных полупроводниках главным фактором, определяющим величину удельной проводимости, является концентрация примесных атомов, которая может изменяться на несколько порядков.
Необходимо иметь в виду, что подвижность заряженных частиц зависит от температуры. Эта зависимость связана с тем, что с ростом температуры увеличивается амплитуда тепловых колебаний атомов кристаллической решетки, и соответственно уменьшается длина свободного пробега частиц между соударениями с атомами. В результате снижается их дрейфовая скорость, что при неизменной напряженности поля эквивалентно уменьшению подвижности частиц. Как уже отмечалось, уменьшение подвижности с ростом температуры происходит довольно слабо (в кремнии это происходит пропорционально 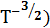 . В результате при постоянной величине концентрации основных носителей (на 2-ом участке приведенного на рис. 1.5 графика) аналогичным образом уменьшается удельная электрическая проводимость.
. В результате при постоянной величине концентрации основных носителей (на 2-ом участке приведенного на рис. 1.5 графика) аналогичным образом уменьшается удельная электрическая проводимость.
На рис. 1.6 приведен график зависимостей подвижности и дрейфовой скорости электронов от напряженности электрического поля (подобным же образом выглядят аналогичные зависимости для дырок). В относительно слабых полях (Е  ) энергия, которую получают частицы от поля на длине свободного пробега, не превышает энергии их теплового движения, равной 3/2 kT. При этом потери энергии частиц при их столкновениях с атомами относительно невелики, и подвижность частиц остается постоянной, а дрейфовая скорость линейно растет с увеличением напряженности поля. В более сильных полях частицы приобретают энергию превышающую энергию теплового движения. В этом случае частицы называют «горячими». При этом потери энергии при столкновениях с атомами настолько увеличиваются, что рост дрейфовой скорости замедляется, что эквивалентно уменьшению подвижности. При Е
) энергия, которую получают частицы от поля на длине свободного пробега, не превышает энергии их теплового движения, равной 3/2 kT. При этом потери энергии частиц при их столкновениях с атомами относительно невелики, и подвижность частиц остается постоянной, а дрейфовая скорость линейно растет с увеличением напряженности поля. В более сильных полях частицы приобретают энергию превышающую энергию теплового движения. В этом случае частицы называют «горячими». При этом потери энергии при столкновениях с атомами настолько увеличиваются, что рост дрейфовой скорости замедляется, что эквивалентно уменьшению подвижности. При Е 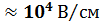 происходит насыщениедрейфовой скорости частиц.В кремнии скорость насыщения составляет
происходит насыщениедрейфовой скорости частиц.В кремнии скорость насыщения составляет 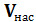
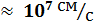 .
.

Рис. 1.6. Зависимости подвижности и дрейфовой скорости электронов от напряженности электрического поля.
Выражения для плотностей электронной и дырочной составляющих диффузионного тока приведены в [1,2]:
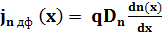 , (1.23)
, (1.23)
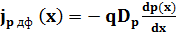 , (1.24)
, (1.24)
где  и
и 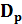 – коэффициенты диффузии электронов и дырок соответственно. Противоположные знаки в выражениях (1.23) и (1.24) отражают противоположное направление электронной и дырочной составляющих диффузионного тока. Следует отметить, что плотности обеих составляющих диффузионного тока определяются градиентами (пространственными производными) соответствующих концентраций. При этом поскольку пространственное распределение концентрации частиц в общем случае может быть нелинейным, градиенты соответствующих концентраций и, следовательно, плотности соответствующих составляющих диффузионного тока являются функциями продольной координаты х.
– коэффициенты диффузии электронов и дырок соответственно. Противоположные знаки в выражениях (1.23) и (1.24) отражают противоположное направление электронной и дырочной составляющих диффузионного тока. Следует отметить, что плотности обеих составляющих диффузионного тока определяются градиентами (пространственными производными) соответствующих концентраций. При этом поскольку пространственное распределение концентрации частиц в общем случае может быть нелинейным, градиенты соответствующих концентраций и, следовательно, плотности соответствующих составляющих диффузионного тока являются функциями продольной координаты х.
Коэффициенты диффузии электронов и дырок линейно связаны с их подвижностями соотношениями Эйнштейна
 =
= 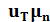 , (1.25)
, (1.25)
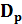 =
= 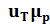 , (1.26)
, (1.26)
где 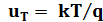 – термический (тепловой, температурный) потенциал. Заметим, что при Т = 300 К
– термический (тепловой, температурный) потенциал. Заметим, что при Т = 300 К  . Линейная связь коэффициентов диффузии с подвижностями частиц позволяет сделать выводы о том, что
. Линейная связь коэффициентов диффузии с подвижностями частиц позволяет сделать выводы о том, что 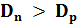 .
.
В общем случае при наличии электрического поля и неравномерного распределения концентрации носителей заряда полный ток в полупроводнике равен
j = 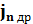 +
+ 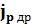 +
+ 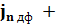
 . (1.27)
. (1.27)
Дата добавления: 2021-01-26; просмотров: 527;











